题目内容
已知函数f(x)=2x3-9ax2+12a2x,(a>0).
(1)若a=1,问函数f(x)图象过原点的切线有几条?求出切线方程;
(2)求函数f(x)在区间[0,2]内的最大值.
(1)若a=1,问函数f(x)图象过原点的切线有几条?求出切线方程;
(2)求函数f(x)在区间[0,2]内的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)f′(x)=6x2-18x+12,由此能求出切线方程为y=12x或y=
x.即共有两条切线过原点.
(2)f′(x)=6x2-18ax+12a2=6(x-a)(x-2a),由此根据a的取值范围利用导数的性质能求出函数f(x)在区间[0,2]内的最大值.
| 15 |
| 8 |
(2)f′(x)=6x2-18ax+12a2=6(x-a)(x-2a),由此根据a的取值范围利用导数的性质能求出函数f(x)在区间[0,2]内的最大值.
解答:
解:(1)a=1,f′(x)=6x2-18x+12,
设切点为(x0,2x03-9x02+12x0),
则切线方程为y-(2x03-9x02+12x0)=(6x02-18x0+12)(x-x0),
∵切线过原点:即2x03-9x02+12x0=(6x02-18x0+12)x0,
∴x0=0或x0=
,
∴切线方程为y=12x或y=
x.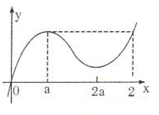
即共有两条切线过原点.
(2)f′(x)=6x2-18ax+12a2=6(x-a)(x-2a),
且f(x)在[0,a]是递增,在[a,2a]上递减,在[2a,+∞)上递增,
f(x)在x=a时有极大值f(a).
①当a>2时,f(x)max=f(2)=24a2-36a+16,
②当1≤a≤2时,f(x)max=f(a)=5a2,
③当0<a<1时,f(a)-f(2)=5a3-24a2+36a-16
=(5a-4)(a-2)2,
f(x)max=
.
综上所述,f(x)max=
.
设切点为(x0,2x03-9x02+12x0),
则切线方程为y-(2x03-9x02+12x0)=(6x02-18x0+12)(x-x0),
∵切线过原点:即2x03-9x02+12x0=(6x02-18x0+12)x0,
∴x0=0或x0=
| 9 |
| 4 |
∴切线方程为y=12x或y=
| 15 |
| 8 |

即共有两条切线过原点.
(2)f′(x)=6x2-18ax+12a2=6(x-a)(x-2a),
且f(x)在[0,a]是递增,在[a,2a]上递减,在[2a,+∞)上递增,
f(x)在x=a时有极大值f(a).
①当a>2时,f(x)max=f(2)=24a2-36a+16,
②当1≤a≤2时,f(x)max=f(a)=5a2,
③当0<a<1时,f(a)-f(2)=5a3-24a2+36a-16
=(5a-4)(a-2)2,
f(x)max=
|
综上所述,f(x)max=
|
点评:本题考查切线方程的求法,考查函数的最大值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目