题目内容
在平面直角坐标系中,过圆x2+y2=1上的动点M作y轴的垂线且交y轴于点N,点Q满足:
=2
-
.
(1)求点Q的轨迹方程C;
(2)设曲线C分别与x,y轴正半轴交于A,B两点,直线y=kx(k>0)与曲线C交于E,F两点,与线段AB交于点D,
=6
,求k值.
| OQ |
| OM |
| ON |
(1)求点Q的轨迹方程C;
(2)设曲线C分别与x,y轴正半轴交于A,B两点,直线y=kx(k>0)与曲线C交于E,F两点,与线段AB交于点D,
| ED |
| DF |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)设M(x0,y0),Q(x,y),则N(0,y0),由
=2
-
,能求出点Q的轨迹方程.
(2)由已知A(2,0),B(0,1),得到直线AB:x+2y=2.设D(x0,kx0),E(x1,kx1),F(x2,kx2),(x1<x2),
由对称性x2=-x1.将y=kx代入方程
+y2=1,得x2=-x1=
,由
=6
,又点D在AB上,能求出k.
| OQ |
| OM |
| ON |
(2)由已知A(2,0),B(0,1),得到直线AB:x+2y=2.设D(x0,kx0),E(x1,kx1),F(x2,kx2),(x1<x2),
由对称性x2=-x1.将y=kx代入方程
| x2 |
| 4 |
| 2 | ||
|
| ED |
| DF |
解答:
解:(1)设M(x0,y0),Q(x,y),则N(0,y0),(2分)
由
=2
-
,得:
,即
,(4分)
代入x2+y2=1,有:
+y2=1.
∴点Q的轨迹方程C:
+y2=1.(6分)
(2)由已知A(2,0),B(0,1),得到直线AB:x+2y=2.(8分)
设D(x0,kx0),E(x1,kx1),F(x2,kx2),(x1<x2),
由对称性x2=-x1.
将y=kx代入方程
+y2=1,得x2=-x1=
.(10分)
由
=6
,得:x0=
=
x2=
,
又点D在AB上,得:x0=
.
由
=
,解得k=
或k=
.(13分)
由
| OQ |
| OM |
| ON |
|
|
代入x2+y2=1,有:
| x2 |
| 4 |
∴点Q的轨迹方程C:
| x2 |
| 4 |
(2)由已知A(2,0),B(0,1),得到直线AB:x+2y=2.(8分)
设D(x0,kx0),E(x1,kx1),F(x2,kx2),(x1<x2),
由对称性x2=-x1.
将y=kx代入方程
| x2 |
| 4 |
| 2 | ||
|
由
| ED |
| DF |
| x1+6x2 |
| 7 |
| 5 |
| 7 |
| 10 | ||
7
|
又点D在AB上,得:x0=
| 2 |
| 1+2k |
由
| 2 |
| 1+2k |
| 10 | ||
7
|
| 2 |
| 3 |
| 3 |
| 8 |
点评:本题考查点的轨迹方程的求法,考查直线的斜率的求法,解题时要认真审题,注意向量知识的合理运用.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
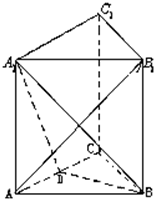 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是