题目内容
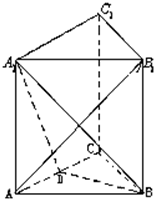如图，三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是| 3 |
（1）求证：平面A1BD⊥平面A1ACC1；
（2）求直线AB1与平面A1BD所成的角的正弦值．
考点：平面与平面垂直的判定,直线与平面所成的角
专题：空间位置关系与距离
分析：（1）由已知条件得AA1⊥底面ABC，BD⊥平面A1ACC1，由此能证明平面A1BD⊥平面A1ACC1．
（2）作AM⊥A1D，设AB1与A1B相交于点P，连接MP，则∠APM就是直线A1B与平面A1BD所成的角，由此能求出直线AB1与平面A1BD所成的角的正弦值．
（2）作AM⊥A1D，设AB1与A1B相交于点P，连接MP，则∠APM就是直线A1B与平面A1BD所成的角，由此能求出直线AB1与平面A1BD所成的角的正弦值．
解答：
（1）证明：∵正三棱住ABC-A1B1C1，∴AA1⊥底面ABC，
又∵BD⊥AC，A1A∩AC=A，∴BD⊥平面A1ACC1，
又∵BD?平面A1BD，
∴平面A1BD⊥平面A1ACC1…6分
（2）解：作AM⊥A1D，M为垂足，
由（1）知AM⊥平面A1DB，设AB1与A1B相交于点P，
连接MP，则∠APM就是直线A1B与平面A1BD所成的角，…9分
∵AA1=
，AD=1，∴在Rt△AA1D中，
∠A1DA=
，∴AM=1×sin60°=
，AP=
AB1=
，
∴sin∠APM=
=
=
．
直线AB1与平面A1BD所成的角的正弦值为
．…12分．
又∵BD⊥AC，A1A∩AC=A，∴BD⊥平面A1ACC1，
又∵BD?平面A1BD，
∴平面A1BD⊥平面A1ACC1…6分
（2）解：作AM⊥A1D，M为垂足，
由（1）知AM⊥平面A1DB，设AB1与A1B相交于点P，
连接MP，则∠APM就是直线A1B与平面A1BD所成的角，…9分
∵AA1=
| 3 |
∠A1DA=
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴sin∠APM=
| AM |
| AP |
| ||||
|
| ||
| 7 |
直线AB1与平面A1BD所成的角的正弦值为
| ||
| 7 |
点评：本题考查平面与平面垂直的证明，考查直线性与平面所成角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
已知F1，F2是椭圆C：
在股票市场上，投资者常参考股价（每一股的价格）的某条平滑均线的变化情况来决定买入或卖出股票．股民老张在研究股票的走势图时，发现一只股票的均线近期走得很有特点：如果按如图所示的方式建立平面直角坐标系xoy，则股价y（元）和时间x的关系在ABC段可近似地用解析式y=asin（ωx+φ）+b（0＜φ＜π）来描述，从C点走到今天的D点，是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线l：x=34对称．老张预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线l对称，EF段是股价延续DE段的趋势（规律）走到这波上升行情的最高点F．现在老张决定取点A（0，22），点B（12，19），点D（44，16）来确定解析式中的常数a，b，ω，φ，并且求得ω=
函数f（x）=sin（ωx+ϕ）（ω＞0，|ϕ|＜