题目内容
已知函数f(x)=2sin(2x-
).
(Ⅰ)请你用“五点法”画出函数f(x)在长度为一个周期的闭区间上的图象;
(Ⅱ)若x∈[
,π]时,求函数f(x)的最值以及取得最值时的x的值.

| π |
| 3 |
(Ⅰ)请你用“五点法”画出函数f(x)在长度为一个周期的闭区间上的图象;
(Ⅱ)若x∈[
| π |
| 2 |

考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的定义域和值域
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图;
(Ⅱ)根据三角函数图象分析函数的单调性,进而可得函数f(x)的最值以及取得最值时的x的值.
(Ⅱ)根据三角函数图象分析函数的单调性,进而可得函数f(x)的最值以及取得最值时的x的值.
解答:
解(Ⅰ):①列表:
②在坐标系中描出以上五点
③用光滑的曲线连接这五点,得所要求作的函数图象如下所示.
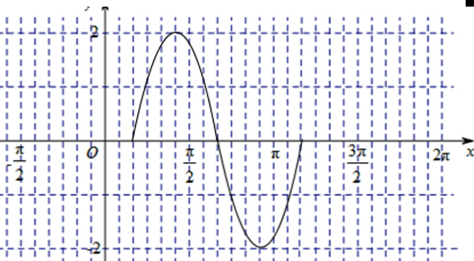
(Ⅱ)由图可知:当x∈[
,
]时,函数为减函数,当x∈[
,π]时,函数为增函数,
故当x=
时,函数取最小值-2,当x=
时,函数取最大值
.
2x-
| 0 |
| π |
| 2π | ||||||||||
| x |
|
|
|
|
| ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |
③用光滑的曲线连接这五点,得所要求作的函数图象如下所示.

(Ⅱ)由图可知:当x∈[
| π |
| 2 |
| 11π |
| 12 |
| 11π |
| 12 |
故当x=
| 11π |
| 12 |
| π |
| 2 |
| 3 |
点评:本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图以及函数图象之间的变化关系.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目