题目内容
7.设f(x)是定义在R上周期为2的函数,且对任意的实数x,恒有f(x)-f(-x)=0,当x∈[0,1]时,f(x)=-$\sqrt{1-{x^2}}$,则函数g(x)=f(x)-ex+1在区间[-2017,2017]上零点的个数为( )| A. | 2016 | B. | 2017 | C. | 4032 | D. | 4034 |
分析 由题意可判断出函数f(x)是周期为2的偶函数,当x∈[-1,1]时,f(x)=-$\sqrt{1-{x^2}}$,在[-2017,0],共有1008个半圆弧及一个$\frac{1}{4}$圆弧,即可得出结论.
解答 解:∵对任意的实数x,恒有f(x)-f(-x)=0,
∴函数f(x)是周期为2的偶函数,
∵当x∈[0,1]时,f(x)=-$\sqrt{1-{x^2}}$,
∴当x∈[-1,1]时,f(x)=-$\sqrt{1-{x^2}}$,
在[-2017,0],共有1008个半圆弧及一个$\frac{1}{4}$圆弧,
∴函数g(x)=f(x)-ex+1在区间[-2017,2017]上零点的个数为1008×2+1=2017,
故选:B.
点评 本题主要考查函数与方程的应用,根据条件判断函数的奇偶性和函数在一个周期内的图象是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知△ABC的三内角A、B、C所对的边分别是a、b、c,设向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(sinB,sinA),若$\overrightarrow{m}$$∥\overrightarrow{n}$,且满足(2a-c)cosB=bcosC,则△ABC的形状是( )
| A. | 等腰直角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 直角三角形, |
15.已知集合A={x|log2x>0},B={x|x<2},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
12.已知向量$\overrightarrow a=({1-t\;\;,\;\;2t-1\;\;,\;\;0})$,$\overrightarrow b=({2\;\;,\;\;t\;\;,\;\;t})$(t∈R),则$|{\overrightarrow b-\overrightarrow a}|$的最小值是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
17.若集合A={x|1≤2x≤16},B={x|log3(x2-2x)>1},则A∩B等于( )
| A. | (3,4] | B. | [3,4] | C. | (-∞,0)∪(0,4] | D. | (-∞,-1)∪(0,4] |
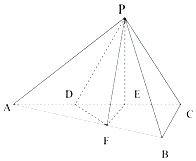 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.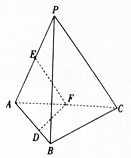 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: