题目内容
在平面四边形ABCD中，顺次的三条线段AC=CD=DA=10，AB=8，BC=6，求（BD+AC）•（BD-AC）的值．
考点：余弦定理
专题：解三角形
分析：如图所示，由AC=10，AB=8，BC=6，可得∠ABC=90°．设∠ACB=θ，则sinθ=
=
，cosθ=
．可得cos∠BCD=cos（θ+60°）．利用余弦定理可得：BD2=DC2+BC2-2DC•BC•cos（θ+60°），再利用平方差公式可得（BD+AC）•（BD-AC）=BD2-AC2．
| 8 |
| 10 |
| 4 |
| 5 |
| 3 |
| 5 |
解答：
解：如图所示，
∵AC=10，AB=8，BC=6，62+82=102，
∴∠ABC=90°．
设∠ACB=θ，则sinθ=
=
，cosθ=
．
∴cos∠BCD=cos（θ+60°）=cosθcos60°-sinθsin60°=
×
-
×
=
．
∴BD2=DC2+BC2-2DC•BC•cos（θ+60°）=102+62-2×10×6×
=100+48
，
∴（BD+AC）•（BD-AC）=BD2-AC2=100+48
-102=48
．
∵AC=10，AB=8，BC=6，62+82=102，
∴∠ABC=90°．
设∠ACB=θ，则sinθ=
| 8 |
| 10 |
| 4 |
| 5 |
| 3 |
| 5 |
∴cos∠BCD=cos（θ+60°）=cosθcos60°-sinθsin60°=
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
3-4
| ||
| 10 |
∴BD2=DC2+BC2-2DC•BC•cos（θ+60°）=102+62-2×10×6×
3-4
| ||
| 10 |
| 3 |
∴（BD+AC）•（BD-AC）=BD2-AC2=100+48
| 3 |
| 3 |
点评：本题考查了直角三角形的边角关系、两角和差的余弦公式、余弦定理、平方差公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
函数y=
的图象大致是（ ）
| x3 |
| 2x-1 |
A、 |
B、 |
C、 |
D、 |
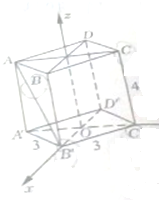已知长方体ABCD-A′B′C′D′的上，下底面都是边长为3的正方形，长方体的高为4，如图建立空间直角坐标系，求下列直线的一个方向向量．