题目内容
已知tanα=
，求
的值．
| 1 |
| 2 |
| 2cosα-3sinα |
| 3cosα+4sinα |
考点：三角函数的化简求值
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系，求得
的值．
| 2cosα-3sinα |
| 3cosα+4sinα |
解答：
解：∵tanα=
，∴
=
=
．
| 1 |
| 2 |
| 2cosα-3sinα |
| 3cosα+4sinα |
| 2-3tanα |
| 3+4tanα |
| 1 |
| 10 |
点评：本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
相关题目
函数f（x）=
的定义域为R，则实数a的取值范围是（ ）
| 1 |
| ax2+4ax+3 |
A、[0，
| ||
B、（0，
| ||
C、（
| ||
| D、（-∞，0） |
函数f（x）=xlnx在点x=1处的导数为（ ）
| A、-1 | B、0 | C、1 | D、2 |
圆心在（a，
），半径为a 的圆的极坐标方程为（ ）
| π |
| 2 |
| A、ρ=acosθ |
| B、ρ=2acosθ |
| C、ρ=asinθ |
| D、ρ=2asinθ |
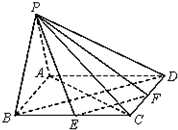如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PB=PD，且EF分别是BC，CD的中点．求证：