题目内容
9．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}-2x+1（x≤0）}\\{|lo{g}_{2}x|（x＞0）}\end{array}\right.$，若方程f（x）=k有四个不同的实数根，x1、x2、x3、x4，则x1+x2+x3+x4的取值范围是（ ）| A． | [0，$\frac{1}{2}$] | B． | [$\frac{1}{2}$，$\frac{9}{4}$） | C． | [$\frac{1}{2}$，$\frac{9}{4}$] | D． | [$\frac{9}{4}$，+∞） |
分析 由题意，当1＜k＜2时，方程有四个不同的解，且x1+x2=-2，x3x4=1且2≤x4＜4，从而结合基本不等式及函数的单调性求解．
解答 解：由题意，当1＜k＜2时，方程有四个不同的解，
且x1+x2=-2，x3x4=1且2≤x4＜4；
故2+$\frac{1}{2}$≤x3+x4＜4+$\frac{1}{4}$，
故$\frac{1}{2}$≤x1+x2+x3+x4＜$\frac{9}{4}$，
即x1+x2+x3+x4的取值范围是[$\frac{1}{2}$，$\frac{9}{4}$），
故选B．
点评 本题考查了函数与方程、不等式的关系，同时考查了数形结合的思想方法应用，属于中档题．
练习册系列答案
相关题目
6．下列命题正确的是（ ）
| A． | 若两条直线和同一个平面平行，则这两条直线平行 | |
| B． | 若一直线与两个平面所成的角相等，则这两个平面平行 | |
| C． | 若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 | |
| D． | 若两个平面垂直于同一个平面，则这两个平面平行 |
7．
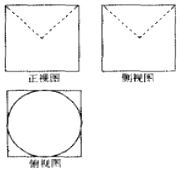某几何体的三视图如图所示，图中四边形都是边长为2的正方形，两条虚线相互垂直，则该几何体的表面积是（ ）
某几何体的三视图如图所示，图中四边形都是边长为2的正方形，两条虚线相互垂直，则该几何体的表面积是（ ）| A． | $24+（{\sqrt{2}+1}）π$ | B． | $24+（{\sqrt{2}-1}）π$ | C． | $24-（{\sqrt{2}+1}）π$ | D． | $24-（{\sqrt{2}-1}）π$ |
4．已知命题p：?x∈R，2x+$\frac{1}{{2}^{x}}$＞2，命题q：?x∈[0，$\frac{π}{2}$]，使sinx+cosx=$\frac{1}{2}$，则下列命题中为真命题的是（ ）
| A． | ￢p∧￢q | B． | ￢p∧q | C． | p∧￢q | D． | p∧q |
1．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的焦点为F1，F2，且C上的点P满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0，|PF1|=3，|PF2|=4，则双曲线C的离心率为（ ）
| A． | $\frac{{\sqrt{10}}}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{5}{2}$ | D． | 5 |