题目内容
12.设等差数列{an}前n项和为Sn,且a5+a6=24,S11=143.(1)求数列{an}的通项公式;
(2)记bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{bn}的前n项和Tn.
分析 (1)设等差数列{an}的首项为a1,公差为d,由已知列方程组求得首项和公差,代入等差数列的通项公式求得答案;
(2)把(1)中求得的通项公式代入bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,然后利用裂项相消法求得数列{bn}的前n项和Tn.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
由a5+a6=24,S11=143,
得$\left\{\begin{array}{l}{2{a}_{1}+9d=24}\\{11({a}_{1}+5d)=143}\end{array}\right.$,解得a1=3,d=2.
∴an=3+2(n-1)=2n+1;
(2)bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n+1)(2n+3)}=\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,
∴Tn=b1+b2+…+bn=$\frac{1}{2}(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n+1}-\frac{1}{2n+3})$=$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+3})$=$\frac{n}{6n+9}$.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,训练了裂项相消法求数列的前n项和,是中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
3.已知变量x,y之间的线性回归方程为$\widehat{y}$=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
| x | 6 | 8 | 10 | 12 |
| y | 6 | m | 3 | 2 |
| A. | 变量x,y之间呈现负相关关系 | |
| B. | m=4 | |
| C. | 可以预测,当x=11时,y=2.6 | |
| D. | 由表格数据知,该回归直线必过点(9,4) |
17.已知x,y的取值如表所示:从散点图分析,x与y线性相关,且$\widehat{y}$=kx+1,则k=0.8.
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
2.将函数f(x)=cos(ωx-$\frac{π}{2}}$)(ω>0)的图象向右平移$\frac{π}{4}$个单位长度,所得的图象经过点$({\frac{3π}{4},0})$,则ω的最小值是( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | 2 |
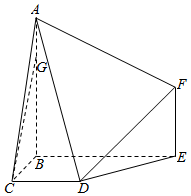 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1. 如图,四棱锥P-ABCD的底面为平行四边形,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,M为PC中点.