Question

【题目】关于的方程的实根个数记.（1）若，则=____________；（2）若，存在使得成立，则的取值范围是_____.

Answer 1

【答案】

【解析】

（1）根据一次函数的特点直接可得到此时的值；

（2）利用函数图象先考虑是否满足，再利用图象分析时满足要求时对应的不等式，从而求解出的取值范围.

（1）若g（x）=x+1，则函数的值域为R，且函数为单调函数，故方程g（x）=t有且只有一个根，故f（t）=1，

（2）

当时，利用图象分析可知：

如下图，此时，，不满足题意；

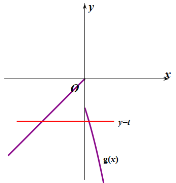
如下图，此时，，不满足题意；

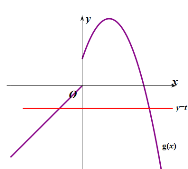
当时，利用图象分析可知：

当时，由上面图象分析可知不符合题意，

当时，若要满足，如下图所示：

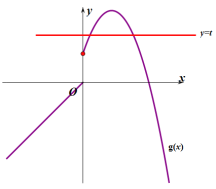
只需满足：，，所以，解得.

综上可知：.

故答案为：；.