题目内容
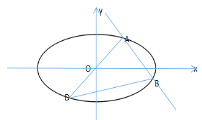
【题目】已知椭圆
的中心在原点，焦点在
轴上，短轴长和焦距都等于2，
是椭圆上的一点，且在第一象限内，过且斜率等于
的直线与椭圆交于另一点
，点关于原点的对称点为
.
（1）求椭圆的方程；
（2）证明：直线
的斜率为定值；
（3）求
面积的最大值．
【答案】（1）
（2）详见解析；（3）
【解析】
（1）设椭圆的方程，根据椭圆的性质即可求得
和
的值，求得椭圆方程；
（2）利用点差法即可求证直线
的斜率为定值；
（3）设直线的方程，由
，将直线的方程代入椭圆方程，利用韦达定理及弦长公式及基本不等式即可求得
面积的最大值．
（1）由题意可设椭圆
的方程为
，
，则
，
所以的方程为；
（2）设
，
，
，
，则
，
，直线的斜率
，
由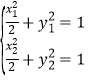
，两式相减，
，
由直线
，所以
，
直线的斜率为定值；
（3）因为
，
关于原点对称，所以，
由（1）可知的斜率
，设方程为
且
，
到的距离
由
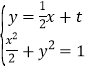，整理得：
，
所以
，
所以
，
，
，
当且仅当
，即
时等号成立，所以面积的最大值为.
练习册系列答案
相关题目
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位：千元/平方米)的统计数据如下表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
（1）求
关于x的线性回归方程；
（2）利用（1）中的回归方程，分析2011年至2017年该市新开楼盘平均销售价格的变化情况，并预测该市2019年新开楼盘的平均销售价格。
附：参考公式：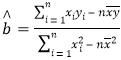 
，
，其中
为样本平均值。
参考数据：
．
