题目内容
5.坐标平面上的点集S满足S=$\{(x,y)|{log_2}({y^2}-y+2)=2{sin^4}x+2{cos^4}x,-\frac{π}{8}≤x≤\frac{π}{4}\}$,将点集S中的所有点向y轴作投影,所得投影线段的总长度为( )| A. | 1 | B. | $\frac{{\sqrt{3}+\sqrt{5}}}{2}$ | C. | $\sqrt{8\sqrt{2}-7}$ | D. | 2 |
分析 先求出2sin4x+2cos4x=2-4sin2x•cos2x=2-(sin2x)2的范围,即可得出函数x=log2(y2-y+2)的值域范围,从而求出函数函数x=log2(y2-y+2)的定义域,进一步可求投影长度.
解答 解:1=(sin2x+cos2x)2=sin4x+cos4x+2sin2x•cos2x,
∴2sin4x+2cos4x=2-4sin2x•cos2x=2-(sin2x)2,
∵x∈[-$\frac{π}{8}$,$\frac{π}{4}$],∴2x∈[-$\frac{π}{4}$,$\frac{π}{2}$],∴-$\frac{\sqrt{2}}{2}$≤sin2x≤1,
∴2-(sin2x)2∈[1,2]
∴log2(y2-y+2)∈[1,2],
∴2≤y2-y+2≤4,
∴-1≤y≤0,或1≤y≤2
故y的投影长度为1+1=2,
故选:D.
点评 本题综合考查函数定义域与值域问题,考查的较为灵活,做题中要注意转化.

练习册系列答案
相关题目
6.已知在△ABC中,AB=2,AC=1,∠A=60°,M在边AB上,$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$,则$\overrightarrow{CM}$•$\overrightarrow{CB}$=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 1 | D. | -1 |
13.已知$\overrightarrow{a}$、$\overrightarrow{b}$不平行,且$\overrightarrow{a}$•$\overrightarrow{b}$≠0,且$\overrightarrow{c}$=$\overrightarrow{a}$-($\frac{\overrightarrow{a}•\overrightarrow{a}}{\overrightarrow{a}•\overrightarrow{b}}$)$\overrightarrow{b}$,则向量$\overrightarrow{a}$与$\overrightarrow{c}$夹角为( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
10.某校拟在高一年级开设英语口语选修课,该年级男生600人,女生480人.按性别分层抽样,抽取90名同学做意向调查.
(I)求抽取的90名同学中的男生人数;
(Ⅱ)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
(I)求抽取的90名同学中的男生人数;
(Ⅱ)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?
| 愿意选修英语口语课程有效 | 不愿意选修英语口语课程 | 合计 | |
| 男生 | 25 | 25 | 50 |
| 女生 | 30 | 10 | 40 |
| 合计 | 55 | 35 | 90 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
17.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间为( )
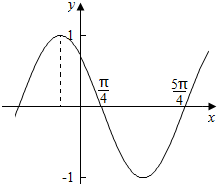

| A. | (kπ+$\frac{3}{4}$π,kπ+$\frac{7}{4}$π),k∈Z | B. | (kπ+$\frac{π}{4}$,kπ+$\frac{5π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{5}{4}$π),k∈Z | D. | (2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),k∈Z |
14.阅读如图所示的程序框图,运行相应的程序,若输出的S为$\frac{11}{12}$,则判断框中填写的内容可以是( )


| A. | n<5 | B. | n<6 | C. | n≤6 | D. | n<9 |