题目内容
18.设正三棱锥A-BCD的所有顶点都在球O的球面上,BC=1,E、F分别是AB,BC的中点,EF⊥DE,则球O的半径为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
分析 根据EF与DE的垂直关系,结合正棱锥的性质,判断三条侧棱互相垂直,再求得侧棱长,根据体积公式计算即可
解答 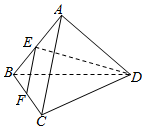 解∵E、F分别是AB、BC的中点,∴EF∥AC,又∵EF⊥DE,
解∵E、F分别是AB、BC的中点,∴EF∥AC,又∵EF⊥DE,
∴AC⊥DE,
取BD的中点O,连接AO、CO,∵三棱锥A-BCD为正三棱锥,
∴AO⊥BD,CO⊥BD,∴BD⊥平面AOC,又AC?平面AOC,∴AC⊥BD,
又DE∩BD=D,∴AC⊥平面ABD;
∴AC⊥AB,
设AC=AB=AD=x,则x2+x2=1⇒x=$\frac{\sqrt{2}}{2}$;
所以三棱锥对应的长方体的对角线为$\sqrt{3(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{6}}{2}$,
所以它的外接球半径为$\frac{\sqrt{6}}{4}$;
故选:B.
点评 本题考查了正三棱锥的外接球半径求法,关键是求出三棱锥的三条侧棱长度,得到对应的长方体对角线,即外接球的直径.

练习册系列答案
相关题目
6.在空间直角坐标系0-xyz中,A(0,0,2),B(0,2,0),C(2,2,2),则三棱锥O-ABC外接球的表面积为( )
| A. | 3π | B. | 4$\sqrt{3}$π | C. | 12π | D. | 48π |
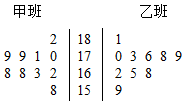 从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.
从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.