题目内容
10.已知数列{an}是等比数列,其前n项和为Sn,满足S2+a1=0,a3=12.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在正整数n,使得Sn>2016?若存在,求出符合条件的n的最小值;若不存在,说明理由.
分析 (Ⅰ)通过设数列{an}的公比为q,利用2a1+a1q=0及a1≠0可知q=-2,进而通过a3=12可知首项a1=3,计算即得结论;
(Ⅱ)通过(I)、利用等比数列的求和公式计算可知Sn>2016等价于(-2)n<-2015,分n为奇数、偶数两种情况讨论即可.
解答 解:(Ⅰ)设数列{an}的公比为q,
因为S2+a1=0,所以2a1+a1q=0,
因为a1≠0,所以q=-2,
又因为${a_3}={a_1}{q^2}=12$,所以a1=3,
所以${a_n}=3×{(-2)^{n-1}}$;
(Ⅱ)结论:符合条件的n的最小值为11.
理由如下:
由(I)可知${S_n}=\frac{{3×[{1-{{(-2)}^n}}]}}{1-(-2)}=1-{(-2)^n}$,
令Sn>2016,即1-(-2)n>2016,整理得(-2)n<-2015,
当n为偶数时,原不等式无解;
当n为奇数时,原不等式等价于2n>2015,解得n≥11;
综上所述,所以满足Sn>2016的正整数n的最小值为11.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
18.设正三棱锥A-BCD的所有顶点都在球O的球面上,BC=1,E、F分别是AB,BC的中点,EF⊥DE,则球O的半径为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
15.已知数列{an}满足:an+1+2an=0,且a2=2,则{an}前10项和等于( )
| A. | $\frac{1-{2}^{10}}{3}$ | B. | -$\frac{1-{2}^{10}}{3}$ | C. | 210-1 | D. | 1-210 |
2.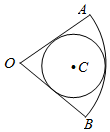 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )| A. | 450 | B. | 400 | C. | 200 | D. | 100 |
19.若实数x,y满足约束条件$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{4x-y+1≥0}\end{array}\right.$则目标函数z=$\frac{y+1}{x+3}$的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |