题目内容
已知圆C:x2+y2=1,直线l:y-kx-1=0
(1)k=1时判断圆C和直线的位置关系.
(2)若圆C上有且仅有三个点到l的距离为
,求实数k的值.
(1)k=1时判断圆C和直线的位置关系.
(2)若圆C上有且仅有三个点到l的距离为
| 1 |
| 2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)k=1时,直线l:y-x-1=0,求出圆C:x2+y2=1的圆心C和半径,利用圆心C到直线y-x-1=0的距离与圆的半径的大小关系能判断圆C和直线l的位置关系.
(2)由圆C上有且仅有三个点到l的距离为
,得到圆心C(0,0)到直线l:y-kx-1=0的距离为
,由此能求出结果.
(2)由圆C上有且仅有三个点到l的距离为
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)k=1时,直线l:y-x-1=0,
圆C:x2+y2=1的圆心C(0,0),半径r=1,
圆心C(0,0)到直线y-x-1=0的距离:
d=
=
<r=1,
∴k=1时圆C和直线相交.
(2)∵圆C:x2+y2=1,直线l:y-kx-1=0,
圆C上有且仅有三个点到l的距离为
,
∴圆心C(0,0)到直线l:y-kx-1=0的距离为
,
∴
=
,
解得k=±
.
∴k=±
.
圆C:x2+y2=1的圆心C(0,0),半径r=1,
圆心C(0,0)到直线y-x-1=0的距离:
d=
| |-1| | ||
|
| ||
| 2 |
∴k=1时圆C和直线相交.
(2)∵圆C:x2+y2=1,直线l:y-kx-1=0,
圆C上有且仅有三个点到l的距离为
| 1 |
| 2 |
∴圆心C(0,0)到直线l:y-kx-1=0的距离为
| 1 |
| 2 |
∴
| |-1| | ||
|
| 1 |
| 2 |
解得k=±
| 3 |
∴k=±
| 3 |
点评:本题考查直线与圆的位置关系的判断,考查实数值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
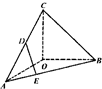 如图,在四面体ABCD中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=
如图,在四面体ABCD中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=