题目内容
4.已知等差数列{an}满足a3=7,a5+a7=26,其前n项和为Sn.(Ⅰ)求{an}的通项公式及Sn;
(Ⅱ)令bn=$\frac{1}{{{S_n}-n}}$(n∈N*),求数列{bn}的前8项和.
分析 (I)利用等差数列的通项公式及其前n项和公式即可得出;
(II)利用“裂项求和”方法即可得出.
解答 解:(Ⅰ)设等差数列{an} 的公差为d,由a5+a7=26,得a6=13,又a6-a3=3d=6,解得d=2.
∴an=a3+(n-3)d=7+2(n-3)=2n+1.
∴以${S_n}=\frac{{{a_1}+{a_n}}}{2}×n=\frac{3+2n+1}{2}×n={n^2}+2n$.
(Ⅱ)由${b_n}=\frac{1}{{{S_n}-n}}$,得${b_n}=\frac{1}{{{n^2}+n}}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$.
设{bn} 的前n 项和为Tn,则${T_8}=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{8}-\frac{1}{9})=1-\frac{1}{9}=\frac{8}{9}$.
故数列{bn} 的前8项和为$\frac{8}{9}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知直线l经过点A(1,-2),B(-3,2),则直线l的方程是( )
| A. | x+y+1=0 | B. | x-y+1=0 | C. | x+2y+1=0 | D. | x+2y-1=0 |
12.在空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,0,0),(2,1,1),(0,1,1).若画该四面体三视图时,正视图以zOy平面为投影面,则得到的侧视图是( )
| A. |  | B. | 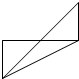 | C. | 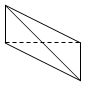 | D. | 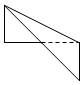 |
19.已知复数z=i(1+i),则|z|等于( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
9.某地区人民法院每年要审理大量案件,去年审理的四类案件情况如表所示:
其中结案包括:法庭调解案件、撤诉案件、判决案件等.根据以上数据,回答下列问题.
(Ⅰ)在编号为1、2、3的收案案件中随机取1件,求该件是结案案件的概率;
(Ⅱ)在编号为2的结案案件中随机取1件,求该件是判决案件的概率;
(Ⅲ)在编号为1、2、3的三类案件中,判决案件数的平均数为$\overline x$,方差为S12,如果表中n=$\overline x$,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).
| 编号 | 项目 | 收案(件) | 结案(件) | |
| 判决(件) | ||||
| 1 | 刑事案件 | 2400 | 2400 | 2400 |
| 2 | 婚姻家庭、继承纠纷案件 | 3000 | 2900 | 1200 |
| 3 | 权属、侵权纠纷案件 | 4100 | 4000 | 2000 |
| 4 | 合同纠纷案件 | 14000 | 13000 | n |
(Ⅰ)在编号为1、2、3的收案案件中随机取1件,求该件是结案案件的概率;
(Ⅱ)在编号为2的结案案件中随机取1件,求该件是判决案件的概率;
(Ⅲ)在编号为1、2、3的三类案件中,判决案件数的平均数为$\overline x$,方差为S12,如果表中n=$\overline x$,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).