题目内容
3.已知$\overrightarrow a$=(1,1,1),$\overrightarrow b$=(0,y,1)(0≤y≤1),则cos<$\overrightarrow a$,$\overrightarrow b$>最大值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 【解法一】利用作图法,构造正方体,考虑极端情况,可快速得出答案;
【解法二】根据两向量的数量积求出夹角的余弦值cos<$\overrightarrow a$,$\overrightarrow b$>,再利用换元法求出它的最大值即可.
解答 解:【解法一】利用作图法,构造正方体,设正方体的边长为1,
如图所示;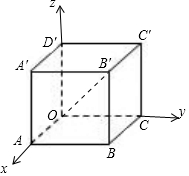
则$\overrightarrow{a}$=$\overrightarrow{OB′}$=(1,1,1),
$\overrightarrow{b}$=$\overrightarrow{OE}$=(0,y,1),且E在线段D′C′上移动,
当E在D′位置时,cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{1×0+1×0+1×1}{\sqrt{{1}^{2}{+1}^{2}{+1}^{2}}×\sqrt{{0}^{2}{+0}^{2}{+1}^{2}}}$=$\frac{\sqrt{3}}{3}$;
当E在C′位置时,cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{1×0+1×1+1×1}{\sqrt{3}×\sqrt{2}}$=$\frac{\sqrt{6}}{3}$为最大值.
【解法二】∵$\overrightarrow a$=(1,1,1),$\overrightarrow b$=(0,y,1)(0≤y≤1),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=y+1,
|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=$\sqrt{{y}^{2}+1}$,
∴cos<$\overrightarrow a$,$\overrightarrow b$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{y+1}{\sqrt{3}•\sqrt{{y}^{2}+1}}$;
设t=$\sqrt{{y}^{2}+1}$,则t2-1=y2,
∴y=$\sqrt{{t}^{2}-1}$(1≤t≤$\sqrt{2}$),
∴f(t)=$\frac{1}{\sqrt{3}}$•$\frac{\sqrt{{t}^{2}-1}+1}{t}$=$\frac{1}{\sqrt{3}}$($\sqrt{1-\frac{1}{{t}^{2}}}$+$\frac{1}{t}$);
设sinα=$\frac{1}{t}$,则1≥sinα≥$\frac{\sqrt{2}}{2}$,即$\frac{π}{4}$≤α≤$\frac{π}{2}$,
∴g(α)=$\frac{1}{\sqrt{3}}$($\sqrt{1{-sin}^{2}α}$+sinα)
=$\frac{1}{\sqrt{3}}$(cosα+sinα)
=$\frac{\sqrt{2}}{\sqrt{3}}$sin(α+$\frac{π}{4}$),
∴当α=$\frac{π}{4}$时,g(α)取得最大值为$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
故选:D.
点评 本题考查了利用向量的数量积求夹角的应用问题,也考查了函数在闭区间上的最值问题,是基础题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | [$\sqrt{3}$,2$\sqrt{3}$] | B. | [$\sqrt{3}$,2$\sqrt{3}$) | C. | ($\sqrt{3}$,2$\sqrt{3}$] | D. | ($\sqrt{3}$,2$\sqrt{3}$) |
| A. | x+y+1=0 | B. | x-y+1=0 | C. | x+2y+1=0 | D. | x+2y-1=0 |
| A. | 30° | B. | 90° | C. | 60° | D. | 45° |
| A. | 2014 | B. | 2015 | C. | 1 | D. | 0 |