题目内容
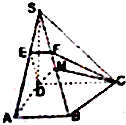 在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=| 2 |
(1)求证:四边形EFCD为直角梯形;
(2)求二面角B-EF-C的平面角的正切值;
(2)设SB的中点为M,当
| CD |
| AB |
考点:二面角的平面角及求法,与二面角有关的立体几何综合题
专题:空间角
分析:(1)由CD∥AB,得到CD∥平面SAB,进面得到CD∥EF,再由题设条件推导出CD⊥ED,EF<AB<CO,由此能够证明四边形EFCD为直角梯形.
(2)由已知条件推导出∠AED是二面角B-EF-C的平面角,由此能求出二面角B-EF-C的平面角的正切值.
(3)当
=2时,能使DM⊥MC.由题设条件推导出BC⊥平面SBD.进而得到MD⊥MC,由此得到△DMC为直角三角形.
(2)由已知条件推导出∠AED是二面角B-EF-C的平面角,由此能求出二面角B-EF-C的平面角的正切值.
(3)当
| CD |
| AB |
解答:
解:(1)∵CD∥AB,CD在平面SAB外,AB?平面SAB,
∴CD∥平面SAB,
又∵平面EFCD∩平面SAB=EF,
∴CD∥EF,
∵∠A=∠D=90°,∴CD⊥AD,
∵SD⊥平面ABCD,CD?平面ABCD,
∴CD⊥SD,∵SD∩AD=D,
∴CD⊥平面SAD,
∵ED?平面SAD,∴CD⊥ED,
又∵EF<AB<CO,∴四边形EFCD为直角梯形.
(2)∵CD⊥平面SAD,且CD∥EF,
∴EF⊥平面SAD,∵AE?平面SAD,DE?平面SAD,
∴AE⊥EF,EF⊥DE,
∴∠AED是二面角B-EF-C的平面角,
∵ED⊥CD,∴EC2=ED2+CD2,
又∵AC2=AD2+CD2,且AC=EC,
∴ED=AD=a,∴△ADE是等腰三角形,
∴tan∠AED=tan∠SAD=
=
.
∴二面角B-EF-C的平面角的正切值是
.
(3)当
=2时,能使DM⊥MC.
∵AB=a,∴CD=2a,BD=
=
a,∠BDC=45°,
∴BC=
a,BC⊥BD,
∴SD⊥平面ABCD,∴SD⊥BC,∴BC⊥平面SBD.
在△SBD中,SD=DB,M为SB中点,
∴MD⊥SB.∴MD⊥平面SBC,MC?平面SBC,
∴MD⊥MC,∴△DMC为直角三角形.
∴CD∥平面SAB,
又∵平面EFCD∩平面SAB=EF,
∴CD∥EF,
∵∠A=∠D=90°,∴CD⊥AD,
∵SD⊥平面ABCD,CD?平面ABCD,
∴CD⊥SD,∵SD∩AD=D,
∴CD⊥平面SAD,
∵ED?平面SAD,∴CD⊥ED,
又∵EF<AB<CO,∴四边形EFCD为直角梯形.
(2)∵CD⊥平面SAD,且CD∥EF,
∴EF⊥平面SAD,∵AE?平面SAD,DE?平面SAD,
∴AE⊥EF,EF⊥DE,
∴∠AED是二面角B-EF-C的平面角,
∵ED⊥CD,∴EC2=ED2+CD2,
又∵AC2=AD2+CD2,且AC=EC,
∴ED=AD=a,∴△ADE是等腰三角形,
∴tan∠AED=tan∠SAD=
| SD |
| AD |
| 2 |
∴二面角B-EF-C的平面角的正切值是
| 2 |
(3)当
| CD |
| AB |
∵AB=a,∴CD=2a,BD=
| AB2+AD2 |
| 2 |
∴BC=
| 2 |
∴SD⊥平面ABCD,∴SD⊥BC,∴BC⊥平面SBD.
在△SBD中,SD=DB,M为SB中点,
∴MD⊥SB.∴MD⊥平面SBC,MC?平面SBC,
∴MD⊥MC,∴△DMC为直角三角形.
点评:本题考查棱锥的结构特征,解题时要认真审题,仔细解答,注意空间几何体的合理转化.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
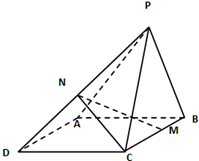 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点. 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,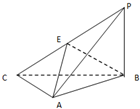 如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.