题目内容

已知
lim
n→∞
（1-qn）=1，则实数q的取值范围是
 
．
考点：极限及其运算
专题：等差数列与等比数列
分析：利用数列极限的定义与性质即可得出．
解答： 解：∵
lim
n→∞
（1-qn）=1，
∴
lim
n→∞
qn=1，故|q|＜1，则q的取值范围为（-1，1）．
故答案为：（-1，1）．
点评：本题考查了数列极限的定义与性质，属于基础题．
练习册系列答案
相关题目
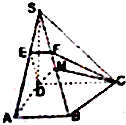在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，S D=
2
a，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F．
（1）求证：四边形EFCD为直角梯形；
（2）求二面角B-EF-C的平面角的正切值；
（2）设SB的中点为M，当
CD
AB
的值是多少时，能使△DMC为直角三角形？请给出证明．
已知函数f（x）=x2+ax+b，且不等式|f（x）|≤2|x2-x-2|对一切x∈R恒成立，则不等式x2+ax+b＜0的解集为
 
．
已知数列{an}为等差数列，a1=1，S5=25，若点P1（1，a3），P2（a4，-3），则直线P1P3的斜率为
 
．
有以下四个命题：①若
1
x
=
1
y
，则x=y．②若lgx有意义，则x＞0．③若x=y，则
x
=
y
．④若x＜y，则 x2＜y2．则是真命题的序号为
 
．
下列四个结论：
①偶函数的图象一定与Y轴相交；
②奇函数的图象一定通过原点；
③f（x）=0（x∈R）既是奇函数，又是偶函数；
④偶函数的图象关于y轴对称．
其中正确的是
 
．（填序号）
已知正数a，b，对任意a＞b且a，b∈（0，1）不等式ax2-ax-a2＞bx2-bx-b2恒成立，则实数x的取值范围是
 
．
已知i是虚数单位，则
3-i
2+i
等于（　　）
A、-1+iB、-1-i
C、1+iD、1-i
在长方体ABCD-A1B1C1D1中，AB=AD=2，AA1=a，E，F分别为AD，CD的中点．
（1）若AC1⊥D1F，求a的值；
（2）若a=2，求二面角E-FD1-D的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网