题目内容
曲线y=x3-2x+4在点（1，3）处的切线方程 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求导函数，然后将点的坐标代入，求出切线斜率，即可求得曲线y=x3-2x+4在点（1，3）处的切线方程．
解答：
解：y=x3-2x+4的导数为：y=3x2-2，
将点（1，3）的坐标代入，即可得斜率为：k=1，
∴曲线y=x3-2x+4在点（1，3）处的切线方程为y-3=x-1，
即x-y+2=0．
故答案为：x-y+2=0．
将点（1，3）的坐标代入，即可得斜率为：k=1，
∴曲线y=x3-2x+4在点（1，3）处的切线方程为y-3=x-1，
即x-y+2=0．
故答案为：x-y+2=0．
点评：本题考查了导数的几何意义，它把函数的导数与曲线的切线联系在一起，使导数成为函数知识与解析几何知识交汇的一个重要载体，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F．求证：△DEF∽△EAF．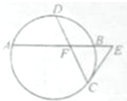
如图，已知圆中两条弦AB与CD相交于点F，且DF=CF=
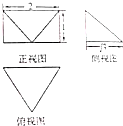
一个几何体的三视图如图所示，其中正视图中△ABC是边长为2的正三角形，俯视图为正六边形，那么该几何体的表面积为