题目内容
10.某几何体的三视图如图所示,若该几何体的所有顶点都在一个球面上,则该球面的表面积为( )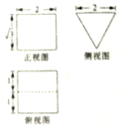
| A. | 20π | B. | $\frac{44}{3}$π | C. | $\frac{28}{3}$π | D. | 4π |
分析 由已知中的三视图可知该几何体是一个三棱柱,求出其外接球半径,可得答案.
解答 解:由已知中的三视图可知该几何体是一个三棱柱,
底面棱长和高均为2,
故底面外接圆半径r=$\frac{2\sqrt{3}}{3}$,球心到底面的距离d=1,
故球半径R=$\sqrt{{d}^{2}+{r}^{2}}$=$\frac{\sqrt{21}}{3}$,
故球的表面积S=4πR2=$\frac{28}{3}$π,
故选:C
点评 本题考查的知识点是球的体积和表面积,球内接多面体,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
20.已知抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,则该抛物线的焦点到准线的距离为( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
2.已知函数f(x)=a-x2(1≤x≤2)与g(x)=2x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,-1] | B. | [-1,1] | C. | [1,3] | D. | [3,+∞] |
19.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“$?{x_0}∈R,x_0^2+{x_0}+1<0$”的否定是“?x∈R,x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
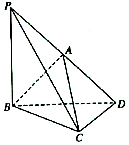 如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP.
如图所示,在三棱锥A-BCD中,A在平面BCD内的投影恰为BD的中点,CD⊥BD,AD⊥AB,延长DA至P,使DA=AP. 如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.
如图,点P为圆E:(x-1)2+y2=r2(r>1)与x轴的左交点,过点P作弦PQ,使PQ与y轴交于PQ的中点D.