题目内容
已知数列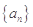 的前
的前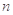 项和为
项和为 ,且满足
,且满足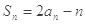 ,
,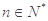
(1)求数列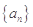 的通项公式;
的通项公式;
(2)求证: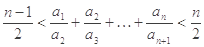
(1) ;(2)
;(2)
解析试题分析:(1)根据题中已知条件 ,得出
,得出 时,
时, 此两式作差整理即可得到形如的数列
此两式作差整理即可得到形如的数列 所满足的关系,从而可求出数列
所满足的关系,从而可求出数列 的通项公式得到所求;
的通项公式得到所求;
(2)
 ,
,
又 ,利用放缩法即可得证.
,利用放缩法即可得证. 
(1)因为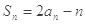 ,………①
,………① ,且
,且 ……… ②
……… ②
①-②得 ,
, 
 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
(2)证明:
 .
. 

∴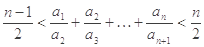 .
.
考点:等比数列,数列的综合应用

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 的前n项和为Sn,若S10=2,S30=14,则S20等于
的前n项和为Sn,若S10=2,S30=14,则S20等于 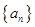 中,
中,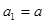 ,
, ,
, ,
, 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且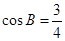 .
.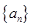 的公比
的公比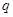 ;
;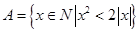 ,且
,且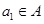 ,求数列
,求数列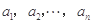 .对
.对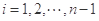 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后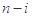 项
项 的最小值记为
的最小值记为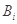 ,
,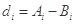 .
.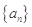 为3,4,7,1,写出
为3,4,7,1,写出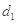 ,
,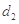 ,
,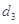 的值;
的值; )是公比大于1的等比数列,且
)是公比大于1的等比数列,且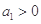 .证明:
.证明: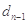 是等比数列.
是等比数列.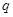 和
和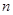 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合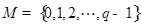 ,集合
,集合 .
.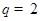 ,
,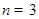 时,用列举法表示集合
时,用列举法表示集合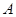 ;
;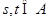 ,
,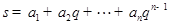 ,
,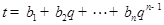 ,其中
,其中 证明:若
证明:若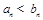 ,则
,则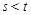 .
.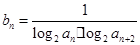 ,
,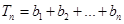 ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得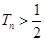 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.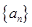 满足:
满足: ,公比
,公比 ,数列
,数列 的前
的前 项和为
项和为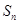 ,且
,且 .
.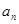 和
和 ;
; ,证明:
,证明: .
.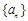 的前n项和为
的前n项和为 满足:
满足: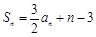 .
.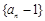 是等比数列;
是等比数列;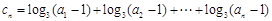 ,对任意
,对任意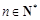 ,是否存在正整数m,使
,是否存在正整数m,使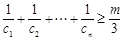 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由.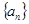 的前n项的和为
的前n项的和为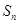 ,且
,且 ,
,
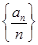 是等比数列
是等比数列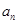 与前n项的和
与前n项的和 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.