题目内容
给定数列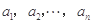 .对
.对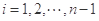 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后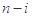 项
项 的最小值记为
的最小值记为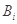 ,
,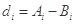 .
.
(1)设数列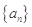 为3,4,7,1,写出
为3,4,7,1,写出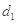 ,
,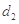 ,
,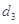 的值;
的值;
(2)设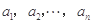 (
( )是公比大于1的等比数列,且
)是公比大于1的等比数列,且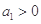 .证明:
.证明: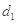 ,
,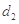 ,…,
,…,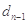 是等比数列.
是等比数列.
(1) ;(2)
;(2) ,即证明是等比数列.
,即证明是等比数列.
解析试题分析:解题思路:(1)利用所给定义,依次求 即可(2)设法证明
即可(2)设法证明 即可.规律总结:凡是新定义性题目,要阅读定义中的信息,与已学知识点相结合,使之转化为学过的知识是解决本类题目的关键.
即可.规律总结:凡是新定义性题目,要阅读定义中的信息,与已学知识点相结合,使之转化为学过的知识是解决本类题目的关键.
试题解析:(1) .
.
(2)因为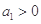 ,公比
,公比 ,所以
,所以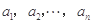 是递增数列.
是递增数列.
因此,对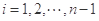 ,
, ,
, .
.
于是对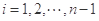 ,
, .
.
因此 且
且 (
( ),即
),即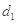 ,
,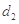 ,,
,,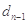 是等比数列.
是等比数列.
考点:1.新定义性题目;2.等比数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
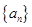 中,已知
中,已知 ,且
,且 ________.
________. 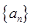 的首项
的首项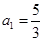 ,
,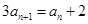 ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数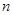 .
.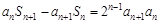 ,
,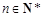 .
.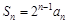 ;
; ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.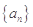 的前
的前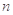 项和为
项和为 ,且满足
,且满足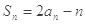 ,
,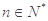
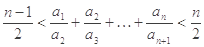
 .
.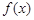 满足:集合
满足:集合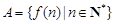 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数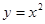 ;②
;②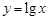 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)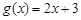 是等比源函数;
是等比源函数;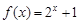 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.