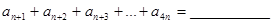题目内容
已知等比数列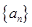 满足:
满足: ,公比
,公比 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列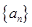 和数列
和数列 的通项
的通项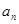 和
和 ;
;
(2)设 ,证明:
,证明: .
.
(1) ,
, ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)利用等比数列的通项公式求出数列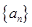 的通项公式,然后先令
的通项公式,然后先令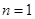 求出
求出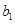 的值,然后在
的值,然后在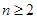 的前提下,由
的前提下,由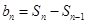 得到
得到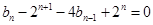 ,解法一是利用构造法得到
,解法一是利用构造法得到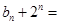
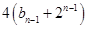 ,构造数列
,构造数列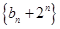 为等比数列,求出该数列的通项公式,从而得出
为等比数列,求出该数列的通项公式,从而得出 的通项公式;解法二是在
的通项公式;解法二是在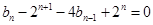 的基础上得到
的基础上得到 ,两边同除以
,两边同除以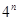 得到
得到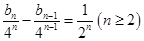 , 利用累加法得到数列
, 利用累加法得到数列 的通项公式,从而得到数列
的通项公式,从而得到数列 的通项公式;(2)利用放缩法得到
的通项公式;(2)利用放缩法得到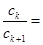
 ,从而证明
,从而证明 ,或者利用不等式的性质得到
,或者利用不等式的性质得到 ,从而证明
,从而证明 .
.
(1)解法一:由 ,
, 得,
得, ,
,
由上式结合 得
得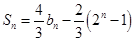 ,
,
则当 时,
时,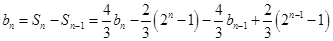 ,
, ,
,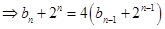 ,
, ,
,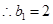 ,
,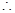 数列
数列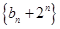 是首项为
是首项为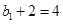 ,公比为
,公比为 的等比数列,
的等比数列,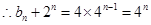 ,
,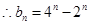 ;
;
解法二:由 ,
, 得,
得, ,
,
由上式结合 得
得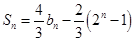 ,
,
则当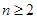 时,
时,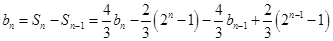 ,
,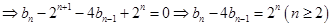 ,
, ,
, ,
, ,
,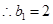 ,
,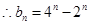 ;
;
(2)由 得
得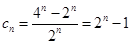 ,
,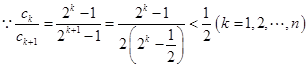 ,
,
或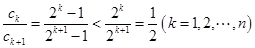
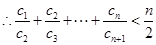 .
.
考点:1.等比数列的通项公式;2.定义法求数列的通项;3.放缩法证明数列不等式

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 ,
, .
.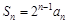 ;
; ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.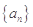 的前
的前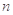 项和为
项和为 ,且满足
,且满足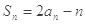 ,
,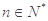
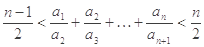
 的前
的前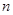 项和为
项和为 ,且
,且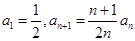 .
.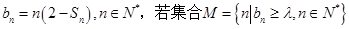 恰有5个元素,求实数
恰有5个元素,求实数 的取值范围.
的取值范围. .
. 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.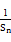 ≤
≤ (n∈N*).
(n∈N*).
 ;
; ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值. 项和为
项和为 ,若
,若 ,则
,则