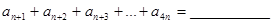题目内容
已知等比数列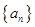 中,
中,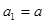 ,
, ,
, ,
, 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且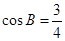 .
.
(1)求数列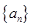 的公比
的公比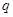 ;
;
(2)设集合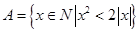 ,且
,且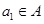 ,求数列
,求数列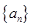 的通项公式.
的通项公式.
(1) 或
或 ;(2)
;(2) 或
或 .
.
解析试题分析:(1)根据题意可知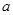 ,
, ,
, 为等比数列
为等比数列 的前三项,因此
的前三项,因此 ,结合条件
,结合条件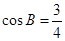 及余弦定理将
及余弦定理将 消去,并且可以得到
消去,并且可以得到 ,即
,即 的值:
的值: ,
, 或
或 ,从而
,从而 或
或 ;(2)条件中的不等式含绝对值号,因此可以考虑两边平方将其去掉:∵
;(2)条件中的不等式含绝对值号,因此可以考虑两边平方将其去掉:∵ ,
,
∴ ,即
,即 ,解得
,解得 且
且 ,从而可得
,从而可得 ,即有
,即有 ,结合(1)及条件等比数列
,结合(1)及条件等比数列 可知通项公式为
可知通项公式为 或
或 .
.
试题解析:(1)∵等比数列 ,
,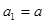 ,
, ,
, ,∴
,∴ , 1分
, 1分
又∵ , 3分
, 3分
而 ,∴
,∴ 或
或 , 5分
, 5分
又∵在△ABC中, , ∴
, ∴ 或
或 ; 6分
; 6分
(2)∵ ,∴
,∴ ,即
,即 ,∴
,∴ 且
且 , 8分
, 8分
又∵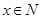 ,∴
,∴ ,∴
,∴ , 10分
, 10分
∴ 或
或 . . 12分
. . 12分
考点:1.等比数列的通项公式;2.余弦定理及其变式;3.解不等式.

练习册系列答案
相关题目
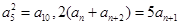 ,则数列{an}的通项公式an =______________。
,则数列{an}的通项公式an =______________。 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为 ,若
,若 ,求实数
,求实数 的值.
的值.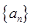 的首项
的首项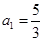 ,
,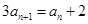 ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数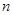 .
.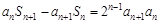 ,
,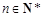 .
.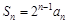 ;
; ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.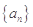 的前
的前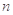 项和为
项和为 ,且满足
,且满足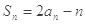 ,
,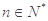
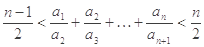

 ;
; ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值. 项和为
项和为 ,若
,若 ,则
,则