题目内容
20.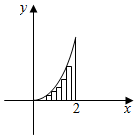 先阅读参考材料,再解决此问题:
先阅读参考材料,再解决此问题:参考材料:求抛物线弧y=x2(0≤x≤2)与x轴及直线x=2围成的封闭图形的面积
解:把区间[0,2]进行n等分,得n-1个分点A($\frac{2i}{n}$,0)(i=1,2,3,…,n-1),过分点Ai,作x轴的垂线,交抛物线于Bi,并如图构造n-1个矩形,先求出n-1个矩形的面积和Sn-1,再求$\underset{lim}{n→∞}$Sn-1,即是封闭图形的面积,又每个矩形的宽为$\frac{2}{n}$,第i个矩形的高为($\frac{2i}{n}$)2,所以第i个矩形的面积为$\frac{2}{n}$•($\frac{2i}{n}$)2;
Sn-1=$\frac{2}{n}$[$\frac{4•{1}^{2}}{{n}^{2}}$+$\frac{4•{2}^{2}}{{n}^{2}}$+$\frac{4•{3}^{2}}{{n}^{2}}$+…+$\frac{4•(n-1)^{2}}{{n}^{2}}$]=$\frac{8}{{n}^{3}}$[12+22+32+…+(n-1)2]=$\frac{8}{{n}^{3}}$•$\frac{n(n-1)(2n-1)}{6}$
所以封闭图形的面积为$\underset{lim}{n→∞}$$\frac{8}{{n}^{3}}$•$\frac{n(n-1)(2n-1)}{6}$=$\frac{8}{3}$
阅读以上材料,并解决此问题:已知对任意大于4的正整数n,不等式$\sqrt{1-\frac{{1}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{2}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{3}^{2}}{{n}^{2}}}$+…+$\sqrt{1-\frac{(n-1)^{2}}{{n}^{2}}}$<an恒成立,则实数a的取值范围为[$\frac{π}{4}$,+∞).
分析 作出f(x)=$\sqrt{1-{x}^{2}}$(0≤x≤1)的图象,可得为以O为原点,1为半径的$\frac{1}{4}$圆.把区间[0,1]进行n等分,得n-1个分点Ai($\frac{i}{n}$,0)(i=1,2,3,…,n-1),过分点Ai,作x轴的垂线,交图象于Bi,并如图构造n-1个矩形,先求出n-1个矩形的面积和Sn-1,再求$\underset{lim}{n→∞}$Sn-1,即是封闭图形的面积,运用圆的面积公式结合恒成立问题的解法,即可得到a的范围.
解答 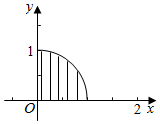 解:作出f(x)=$\sqrt{1-{x}^{2}}$(0≤x≤1)的图象,
解:作出f(x)=$\sqrt{1-{x}^{2}}$(0≤x≤1)的图象,
可得为以O为原点,1为半径的$\frac{1}{4}$圆.
把区间[0,1]进行n等分,得n-1个分点Ai($\frac{i}{n}$,0)(i=1,2,3,…,n-1),
过分点Ai,作x轴的垂线,交图象于Bi,并如图构造n-1个矩形,先求出n-1个矩形的面积和Sn-1,再求$\underset{lim}{n→∞}$Sn-1,即是封闭图形的面积,
又每个矩形的宽为$\frac{1}{n}$,第i个矩形的高为$\sqrt{1-(\frac{i}{n})^{2}}$,
所以第i个矩形的面积为$\frac{1}{n}$•$\sqrt{1-(\frac{i}{n})^{2}}$;
Sn-1=$\frac{1}{n}$[$\sqrt{1-\frac{{1}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{2}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{3}^{2}}{{n}^{2}}}$+…+$\sqrt{1-\frac{(n-1)^{2}}{{n}^{2}}}$],
则封闭图形的面积为$\underset{lim}{n→∞}$=Sn-1=$\frac{π}{4}$•12=$\frac{π}{4}$.
由a>$\frac{1}{n}$[$\sqrt{1-\frac{{1}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{2}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{3}^{2}}{{n}^{2}}}$+…+$\sqrt{1-\frac{(n-1)^{2}}{{n}^{2}}}$]恒成立,
可得a的范围是a≥$\frac{π}{4}$.
故答案为:[$\frac{π}{4}$,+∞).
点评 本题考查数列的求和,注意运用极限的思想方法,考查化简整理整理的运算能力,属于中档题.

(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | 0 | B. | 1 | ||
| C. | 3 | D. | 条件不足,无法计算 |
| A. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| C. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 | |
| D. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 |