题目内容
积分
(-
)dx=( )
| ∫ | a -a |
| a2-x2 |
A、-
| ||
B、-
| ||
| C、πa2 | ||
| D、2πa2 |
考点:定积分
专题:导数的概念及应用
分析:利用微积分基本定理和定积分的几何意义即可求出.
解答:
解:令y=
,则x2+y2=a(y≥0),点(x,y)的轨迹表示半圆,则
dx表示该圆面积的二分之一,
故
dx=
πa2,
故积分
(-
)dx=-
dx=-
πa2,
故选:B
| a2-x2 |
| ∫ | a -a |
| a2-x2 |
故
| ∫ | a -a |
| a2-x2 |
| 1 |
| 2 |
故积分
| ∫ | a -a |
| a2-x2 |
| ∫ | a -a |
| a2-x2 |
| 1 |
| 2 |
故选:B
点评:本题考查定积分的几何意义,熟练掌握微积分基本定理是解题的关键.属基础题.

练习册系列答案
相关题目
曲线y=
x2+
在点(1,1)处切线的倾斜角为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、0° | B、45° |
| C、90° | D、135° |
球的半径是5,则它的体积是( )
| A、400π | ||
| B、100π | ||
C、
| ||
D、
|
为了得到函数y=cos(x+
)的图象,只需要把函数y=cos(x-
)的图象上的所有点( )
| π |
| 4 |
| π |
| 4 |
A、向右平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向左平行移动
|
如图,已知△ABC中,D为BC边上的中点,则下列等式中正确的是( )
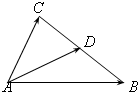

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|