题目内容
已知函数f（x）=
的定义域是一切实数，求m的取值范围．
| ||||
| 2mx2+mx+3 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据题意，应使函数的解析式有意义，即二次根式被开方数大于或等于0，且分母不等于0，列出不等式组，求出m的取值范围．
解答：
解：根据题意，得；
，
即
，
或
；
解得m=0，或0＜m＜1，或1＜m＜24；
∴m的取值范围{m|0≤m＜1，或1＜m＜24}．
|
即
|
或
|
解得m=0，或0＜m＜1，或1＜m＜24；
∴m的取值范围{m|0≤m＜1，或1＜m＜24}．
点评：本题考查了求函数的定义域的问题，解题时应根据题意，列出不等式组，求出问题的答案来，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示程序运行后，输出的值是（ ）
| A、42 | B、43 | C、45 | D、44 |
如图所示的圆盘由八个全等的扇形构成，指针绕中心旋转，可能随机停止则指针停止在阴影部分内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
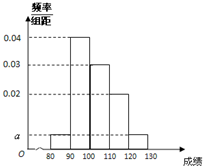为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]