题目内容
5.函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数,设f(x)在[0,1]为非减函数,且满足以下三个条件;①f(0)=0;②f($\frac{x}{3}$)=$\frac{1}{2}$f(x);③f(1-x)=1-f(x),则f($\frac{1}{3}$)+f($\frac{1}{8}$)等于( )| A. | $\frac{1}{128}$ | B. | $\frac{1}{256}$ | C. | $\frac{1}{512}$ | D. | $\frac{3}{4}$ |
分析 由已知函数f(x)满足的三个条件求出f(1),f($\frac{1}{2}$),f($\frac{1}{3}$),进而求出f($\frac{1}{9}$),f($\frac{1}{6}$)的函数值,又由函数f(x)为非减函数,求出f($\frac{1}{8}$)的值,即可得到f($\frac{1}{3}$)+f($\frac{1}{8}$)的值.
解答 解:∵函数f(x)在[0,1]上为非减函数,①f(0)=0;③f(1-x)+f(x)=1,∴f(1)=1,
令x=$\frac{1}{2}$,所以有f($\frac{1}{2}$)=$\frac{1}{2}$.
又∵②f($\frac{x}{3}$)=$\frac{1}{2}$f(x),∴f(x)=2f($\frac{x}{3}$),∴令=1,可得1=2f($\frac{1}{3}$),∴f($\frac{1}{3}$)=$\frac{1}{2}$.
令x=$\frac{1}{2}$,可得f($\frac{1}{6}$)=$\frac{1}{2}$f($\frac{1}{2}$)=$\frac{1}{4}$,令x=$\frac{1}{3}$,可得f($\frac{1}{9}$)=$\frac{1}{2}$f($\frac{1}{3}$)=$\frac{1}{4}$.
∵当x1<x2时都有f(x1)≤f(x2),$\frac{1}{9}$<$\frac{1}{8}$<$\frac{1}{6}$,∴f($\frac{1}{9}$)≤f($\frac{1}{8}$)≤f($\frac{1}{6}$ ),∴f($\frac{1}{8}$)=$\frac{1}{4}$,
∴f($\frac{1}{3}$)+f($\frac{1}{8}$)=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$,
故选:D.
点评 本题主要考查抽象函数、新定义的应用,充分利用题意中非减函数性质,属于中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案①若α⊥γ,β⊥γ,则α∥β;
②若α∥β,m?α,则m∥β;
③若m⊥α,n∥α,则m⊥n;
④若m⊥n,m⊥α,n∥β,则α⊥β.
其中正确命题的序号是( )
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ②③④ |
| A. | 若x<2,则x<1 | B. | 若x≤2,则x≤1 | C. | 若x≤1,则x≤2 | D. | 若x<1,则x<2 |
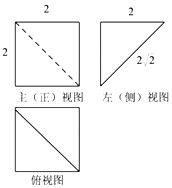
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
| 成绩 | 人数 |
| A | 9 |
| B | 12 |
| C | 31 |
| D | 22 |
| E | 6 |
(1)若该校高二年级共有1000名学生,试估算该校高二年级学生获得成绩为B的人数;
(2)若等级A、B、C、D、E分别对应100分、80分、60分、40分、20分,学校要求“平均分达60分以上”为“教学达标”,请问该校高二年级此阶段教学是否达标?
(3)为更深入了解教学情况,将成绩等级为A、B的学生中,按分层抽样抽取7人,再从中任意抽取2名,求恰好抽到1名成绩为A的概率.
 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2