题目内容
16.设m,n表示两条不同的直线,α,β,γ表示三个不同的平面,给出下列四个命题:①若α⊥γ,β⊥γ,则α∥β;
②若α∥β,m?α,则m∥β;
③若m⊥α,n∥α,则m⊥n;
④若m⊥n,m⊥α,n∥β,则α⊥β.
其中正确命题的序号是( )
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ②③④ |
分析 根据空间中直线与平面,平面与平面的位置关系的几何特征,逐一分析给定四个结论的真假,可得答案.
解答 解:①若α⊥γ,β⊥γ,则α,β可能平行也可能相交,故①错误;
②若α∥β,m?α,则m∥β,故②正确;
③若n∥α,则存在直线a?α,使n∥a,
若m⊥α,则m⊥a,进而m⊥n,故③正确;
④若m⊥n,m⊥α,则n∥α,或n?α,若n∥β,则α,β的关系不能确定,故④错误.
故选:B
点评 本题以命题的真假判断与应用为载体,考查了空间直线与直线,直线与平面的位置关系,难度中档.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
7.下列关于命题的说法错误的是( )
| A. | 在△ABC中,∠A=∠B是sin∠A=sin∠B的充要条件 | |
| B. | 命题“若|x|>|y|,则x>y”的否命题是“若|x|≤|y|,则x≤y” | |
| C. | 复数(a+bi)(1+i)与复数-1+3i相等的充要条件是“a=1,b=2” | |
| D. | 命题“?x∈(0,+∞),2x>1”的否定是“?x0∈(-∞,0],2${\;}^{{x}_{0}}$≤1” |
4.设正实数x,y满足log${\;}_{\frac{1}{2}}$x+log2y=m(m∈[-1,1]),若不等式(x+y)2≤2ax2+(a+1)y2有解,则实数a的取值范围是( )
| A. | a≥1 | B. | a≥$\frac{8}{9}$ | C. | a≥$\frac{7}{8}$ | D. | a≥$\frac{5}{6}$ |
11.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0\;\;,\;\;b>0})$的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | C. | $\frac{x^2}{80}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{20}-\frac{y^2}{80}=1$ |
5.函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数,设f(x)在[0,1]为非减函数,且满足以下三个条件;①f(0)=0;②f($\frac{x}{3}$)=$\frac{1}{2}$f(x);③f(1-x)=1-f(x),则f($\frac{1}{3}$)+f($\frac{1}{8}$)等于( )
| A. | $\frac{1}{128}$ | B. | $\frac{1}{256}$ | C. | $\frac{1}{512}$ | D. | $\frac{3}{4}$ |
6.“a2>b2”是“lna>lnb”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
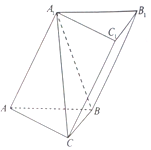 如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.
如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.