题目内容
8. 如图所示是沿圆锥的两条母线将圆锥削去一部分后得几何体的三视图,其体积为$\frac{16π}{9}+\frac{2\sqrt{3}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后得几何体的三视图,其体积为$\frac{16π}{9}+\frac{2\sqrt{3}}{3}$,则圆锥的母线长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
分析 首先还原圆锥被截后的形状,用母线长表示体积,解出l.
解答 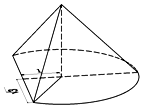 解:由已知三视图得到圆锥的底面半径$r=\sqrt{{1^2}+{{(\sqrt{3})}^2}}=2$,圆锥的高为$\sqrt{{l^2}-{r^2}}=\sqrt{{l^2}-4}$,
解:由已知三视图得到圆锥的底面半径$r=\sqrt{{1^2}+{{(\sqrt{3})}^2}}=2$,圆锥的高为$\sqrt{{l^2}-{r^2}}=\sqrt{{l^2}-4}$,
底面面积$S=\frac{2}{3}π×{2^2}+\frac{1}{2}×2\sqrt{3}×1=\frac{8π}{3}+\sqrt{3}$,
体积$V=\frac{1}{3}(\frac{8π}{3}+\sqrt{3})\sqrt{{l^2}-4}=\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,
故$l=2\sqrt{2}$,
故选A.
点评 本题考查了几何体的三视图;关键是明确几何体的形状.

练习册系列答案
相关题目
9.下列函数中,在区间(-1,1)上既是奇函数又是增函数的是( )
| A. | y=tanx | B. | y=-x3-3x | C. | y=|sinx| | D. | y=$\frac{1}{x+1}$-1 |
3.《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是( )
| A. | $\frac{3π}{10}$ | B. | $\frac{3π}{20}$ | C. | $1-\frac{3π}{10}$ | D. | $1-\frac{3π}{20}$ |
20.若数列{an}满足a1=1,log2an+1=log2an+1(n∈N*),它的前n项和为Sn,则Sn=( )
| A. | 2-21-n | B. | 2n-1-1 | C. | 2n-1 | D. | 2-2n-1 |
17.要得到函数y=$\frac{\sqrt{3}}{2}$sin2x+cos2x-$\frac{1}{2}$的图象,只需将y=sinx图象上所有的点( )
| A. | 横坐标变为原来的一半,纵坐标不变,再向左平移$\frac{π}{6}$个单位 | |
| B. | 横坐标变为原来的两倍,纵坐标不变,再向左平移$\frac{π}{12}$个单位 | |
| C. | 向左平移$\frac{π}{12}$个单位,再将所得各点的横坐标变为原来的两倍,纵坐标不变 | |
| D. | 向左平移$\frac{π}{6}$个单位,再将所得各点的横坐标变为原来的一半,纵坐标不变 |