题目内容
8.已知椭圆的标准方程为$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{\sqrt{3}}{2}$,且椭圆上的点到其中一个焦点最大距离为2+$\sqrt{3}$,抛物线C以原点为顶点,以椭圆与x轴正半轴的交点为焦点.(Ⅰ)求抛物线C的方程;
(Ⅱ)已知点M(2,0),问:x轴上是否存在一定点P,使得对于抛物线C上的任意两点A和B,当$\overrightarrow{AM}$=λ$\overrightarrow{MB}$(λ∈R)时,恒有点M到直线PA与PB的距离相等?若存在,则求点P的坐标,否则说明理由.
分析 (Ⅰ)由题意的离心率公式,即可求得$\sqrt{3}$a=2c,且a+c=2+$\sqrt{3}$,即可求得a和c的值,则b2=a2-c2=1,求得椭圆方程,求得抛物线的焦点坐标,即可求得抛物线C的方程;
(Ⅱ)设直线AB的方程为:x=my+2,代入抛物线方程可得:y2-4my-8=0..由△PAM与△PBM的面积之比等于$\frac{丨PA丨}{丨PB丨}$,可得:PM平分∠APB,因此直线PA,PB的倾斜角互补,即kPA+kPB=0,利用斜率计算公式、根与系数的关系化简即可得出.
解答 解:(1)椭圆的标准方程为$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),焦点在y轴上,
椭圆离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,则$\sqrt{3}$a=2c,①
a+c=2+$\sqrt{3}$,②
解得:a=2,c=$\sqrt{3}$,
则b2=a2-c2=1,
∴椭圆的标准方程:$\frac{{y}^{2}}{4}+{x}^{2}=1$;
则抛物线的焦点坐标为(1,0),抛物线的方程为y2=4x,
∴抛物线的方程为y2=4x;
设动圆圆心的坐标为C(x,y),由题意可得:22+|x|2=(x-2)2+y2,化为:y2=4x.
∴动圆圆心的轨迹方程为:y2=4x.
(Ⅱ)设P(a,0),A(x1,y1),B(x2,y2).
由$\overrightarrow{AM}$=λ$\overrightarrow{MB}$(λ∈R),可知:M,A,B三点共线.
设直线AB的方程为:x=my+2,
$\left\{\begin{array}{l}{x=my+2}\\{{y}^{2}=4x}\end{array}\right.$,整理得:y2-4my-8=0.
由M到PA的距离为d1,由M到PB的距离为d2,
SMPA=$\frac{1}{2}$×丨PA丨×d1,SMPB=$\frac{1}{2}$×丨PB丨×d2,
由M到直线PA与PB的距离相等,
则△PAM与△PBM的面积之比等于$\frac{丨PA丨}{丨PB丨}$,可得:PM平分∠APB,
∴y1+y2=4m,y1•y2=-8.由因此直线PA,PB的倾斜角互补,
∴kPA+kPB=0,∴$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=0,
把x1=my1+2,x2=my2+2,代入可得:$\frac{2m{y}_{1}{y}_{2}+(2-a)({y}_{1}+{y}_{2})}{(m{y}_{1}+2-a)(m{y}_{2}+2-a)}$=0,
∴-16m+(2-a)×4m=0,化为:m(a+2)=0,由于对于任意m都成立,
∴a=-2.
故存在定点(-2,0),满足条件.
点评 本题考查椭圆的标准方程及简单几何性质,直线与抛物线的位置关系,韦达定理,考查计算能力,属于中档题.

| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
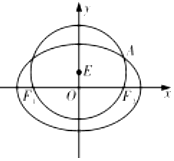 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.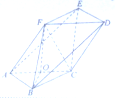 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.