题目内容
某同学离家去学校,为了锻炼身体,开始跑步前进,跑累了再走余下的路程,图中d轴表示该学生离学校的距离,t轴表示所用的时间,则符合学生走法的只可能是( )
A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:数形结合法,函数的性质及应用
分析:根据某学生的行驶情况,先跑步(快速),再步行(慢速),从路程减少的情况来看,先陡后平缓,而图象表示离学校的路程S与时间t之间的函数关系,所以S越来越小,由此即可作出判断.
解答:
解:t=0时,学生在家,离学校的距离d≠0,因此排除A、C;学生先跑后走,因此d随t的变化是先快后慢,
故选D.
故选D.
点评:本小题主要考查函数单调性的应用、函数的图象与图象变化、不等式的解法等基础知识,考查利用函数图象解决实际问题的能力.属于基础题.

练习册系列答案
相关题目
设f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有三个不同的实数解x1、x2、x3,则x
+x
+x
等于( )
|
2 1 |
2 2 |
2 3 |
| A、5 | ||
B、2+
| ||
| C、13 | ||
D、3+
|
甲、乙、丙等6人排成一排,且甲、乙均在丙的同侧,则不同的排法共有( )种(用数字作答).
| A、720 | B、480 |
| C、144 | D、360 |
已知函数f(x)=
,(a>0,且a≠1),若数列{an}满足an=f(n),(n∈N+),且{an}是递增数列,则实数a的取值范围是( )
|
| A、(0,1) | ||
B、[
| ||
| C、(1,3) | ||
| D、(2,3) |
已知变量x,y满足约束条件
,目标函数z=mx+y仅在点(0,1)处取得最小值,则m的取值范围是( )
|
| A、(-∞,4 |
| B、(4,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
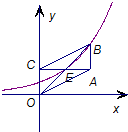 如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )