题目内容
设椭圆的对称中心为坐标原点,其中一个顶点为A(0,2),右焦点F与点B(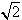 ,
,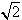 )的距离为2。
)的距离为2。
(1)求椭圆的方程;
(2)是否存在经过点(0,-2)的直线l,使直线l与椭圆相交于不同的两点M,N满足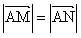 ?若存在,求直线l的倾斜角α;若不存在,请说明理由。
?若存在,求直线l的倾斜角α;若不存在,请说明理由。
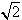 ,
,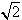 )的距离为2。
)的距离为2。(1)求椭圆的方程;
(2)是否存在经过点(0,-2)的直线l,使直线l与椭圆相交于不同的两点M,N满足
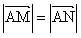 ?若存在,求直线l的倾斜角α;若不存在,请说明理由。
?若存在,求直线l的倾斜角α;若不存在,请说明理由。解:(1)依题意,设椭圆方程为
则其右焦点坐标为
由 2
2
得
即
故
又∵
∴
从而可得椭圆方程为 。
。
(2)由题意可设直线l的方程为

由 知点A在线段MN的垂直平分线上
知点A在线段MN的垂直平分线上
由 消去y得
消去y得
即可得方程 (*)
(*)
由 得方程(*)的
得方程(*)的
即方程(*)有两个不相等的实数根
设 ,
, ,线段MN的中点
,线段MN的中点
则 是方程(*)的两个不等的实根
是方程(*)的两个不等的实根
故有
从而

于是,可得线段MN的中点P的坐标为
又由于
因此直线AP的斜率为

由 得
得
即
解得
即
又
故 或
或
综上可知存在直线l满足题意,其倾斜角 或
或 。
。

则其右焦点坐标为

由
 2
2得

即

故

又∵

∴

从而可得椭圆方程为
 。
。(2)由题意可设直线l的方程为


由
 知点A在线段MN的垂直平分线上
知点A在线段MN的垂直平分线上由
 消去y得
消去y得
即可得方程
 (*)
(*)由
 得方程(*)的
得方程(*)的
即方程(*)有两个不相等的实数根
设
 ,
, ,线段MN的中点
,线段MN的中点
则
 是方程(*)的两个不等的实根
是方程(*)的两个不等的实根故有

从而


于是,可得线段MN的中点P的坐标为

又由于

因此直线AP的斜率为

由
 得
得
即

解得

即

又

故
 或
或
综上可知存在直线l满足题意,其倾斜角
 或
或 。
。
练习册系列答案
相关题目
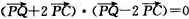 。
。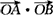 的取值范围。
的取值范围。 ,
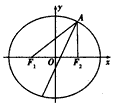
,
 (a>b>0)的离心率是e=
(a>b>0)的离心率是e= ,若点P(0,
,若点P(0, )到椭圆C上的点的最远距离为
)到椭圆C上的点的最远距离为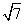 。
。 ),离心率为
),离心率为 ,
,  ,若存在,求直线l的方程;若不存在,请说明理由.
,若存在,求直线l的方程;若不存在,请说明理由.  时,求|MN|的值。
时,求|MN|的值。 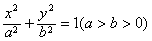 的离心率
的离心率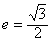 ,连结椭圆的四个顶点得到的菱形的面积为4。
,连结椭圆的四个顶点得到的菱形的面积为4。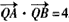 ,求y0的值。
,求y0的值。 ,且它的一个焦点与抛物线y2=-4x的焦点重合,则此椭圆方程为
,且它的一个焦点与抛物线y2=-4x的焦点重合,则此椭圆方程为




 ,则动点P的轨迹方程是
,则动点P的轨迹方程是 


