题目内容
已知平面上一定点C(-1,0)和一定直线l:x=-4,P为该平面上一动点,作PQ⊥l,垂足为Q,且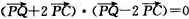 。
。
(1)求点P的轨迹方程;
(2)点O是坐标原点,过点C的直线与点P的轨迹交于A,B两点,求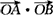 的取值范围。
的取值范围。
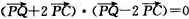 。
。(1)求点P的轨迹方程;
(2)点O是坐标原点,过点C的直线与点P的轨迹交于A,B两点,求
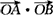 的取值范围。
的取值范围。解:(1)设P(x,y)代入
得点P的轨迹方程为 。
。
(2)设过点C的直线斜率存在时的方程为y= k(x+1),
且 A(x1,y1) ,B(x2,y2)在 上
上
则由

∴ ,
,
∴
∴


∵k2≥0
∴
∴
当过点C的直线斜率不存在时,其方程为x=-1
解得
此时
所以 的取值范围为
的取值范围为 。
。

得点P的轨迹方程为
 。
。(2)设过点C的直线斜率存在时的方程为y= k(x+1),
且 A(x1,y1) ,B(x2,y2)在
 上
上则由


∴
 ,
,
∴

∴



∵k2≥0
∴

∴

当过点C的直线斜率不存在时,其方程为x=-1
解得

此时

所以
 的取值范围为
的取值范围为 。
。
练习册系列答案
相关题目