题目内容
已知椭圆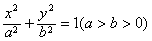 的离心率
的离心率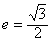 ,连结椭圆的四个顶点得到的菱形的面积为4。
,连结椭圆的四个顶点得到的菱形的面积为4。
(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(-a,0),点Q(0,y0)在线段AB的垂直平分线上,且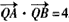 ,求y0的值。
,求y0的值。
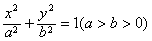 的离心率
的离心率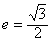 ,连结椭圆的四个顶点得到的菱形的面积为4。
,连结椭圆的四个顶点得到的菱形的面积为4。(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(-a,0),点Q(0,y0)在线段AB的垂直平分线上,且
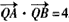 ,求y0的值。
,求y0的值。解:(1)由 得3a2=4c2
得3a2=4c2
再由c2=a2-b2,得a=2b
由题意可知
即ab=2
解方程组
得a=2,b=1
所以椭圆的方程为 ;
;
(2)由(1)可知A(-2,0),设B点的坐标为(x1,y1),直线l的斜率为k,则直线l的方程为y=k(c+2)
于是A、B两点的坐标满足方程组
由方程组消去y并整理,得(1+4k2)x2+16k2x+(16k2-4)=0
由 得
得
从而
设线段AB的中点为M,则M的坐标为
以下分两种情况:
①当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,于是
由 得y0=
得y0=
②当k≠0时,线段AB的垂直平分线方程为

令x=0,解得
由
 ·
·
整理得7k2=2,故
所以
综上 或
或 。
。
 得3a2=4c2
得3a2=4c2再由c2=a2-b2,得a=2b
由题意可知

即ab=2
解方程组

得a=2,b=1
所以椭圆的方程为
 ;
;(2)由(1)可知A(-2,0),设B点的坐标为(x1,y1),直线l的斜率为k,则直线l的方程为y=k(c+2)
于是A、B两点的坐标满足方程组

由方程组消去y并整理,得(1+4k2)x2+16k2x+(16k2-4)=0
由
 得
得
从而

设线段AB的中点为M,则M的坐标为

以下分两种情况:
①当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,于是

由
 得y0=
得y0=
②当k≠0时,线段AB的垂直平分线方程为


令x=0,解得

由

 ·
·
整理得7k2=2,故

所以

综上
 或
或 。
。
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目

 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切.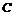 的方程;
的方程; ,
, ,
,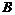 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.