题目内容
20．（$\sqrt{x}$+$\frac{1}{x}$）n的展开式中，第4项的二项式系数与第5项的二项式系数之比为1：3．（1）求展开式中的常数项；
（2）求二项式系数最大的项．
分析 （1）由条件可得$\frac{{C}_{n}^{3}}{{C}_{n}^{4}}$=$\frac{1}{3}$，由此求得n的值．
（2）利用二项展开式的通项公式，二项式系数的性质，求得二项式系数最大的项．
解答 解：（1）∵${（\sqrt{x}+\frac{1}{x}）^n}$的展开式中，第4项的二项式系数与第5项的二项式系数之比为1：3，即$\frac{{C}_{n}^{3}}{{C}_{n}^{4}}$=$\frac{1}{3}$，
求得n=15．
（2）根据展开式的通项公式为Tr+1=${C}_{15}^{r}$•${x}^{\frac{15-3r}{2}}$，可得当r=7或8时，二项式系数${C}_{15}^{r}$取得最大值，
故展开式中二项式系数最大的项为T8=${C}_{15}^{7}$•x-3，T9=${C}_{15}^{8}$•为${C}_{15}^{5}$．${x}^{-\frac{9}{2}}$．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
10．设 a，b∈R，且2a+b=6，则 ${2^a}+{（\sqrt{2}）^b}$的最小值是（ ）
| A． | 6 | B． | $2\sqrt{6}$ | C． | $4\sqrt{2}$ | D． | $2\sqrt{2}$ |
8．若复数z=（cosθ-$\frac{4}{5}$）+（sinθ-$\frac{3}{5}$）i是纯虚数（i为虚数单位），则tan（θ-$\frac{π}{4}$）的值为（ ）
| A． | 7 | B． | $-\frac{1}{7}$ | C． | -7 | D． | -7或$-\frac{1}{7}$ |
15．将八进制数123（8）化为十进制数，结果为（ ）
| A． | 11 | B． | 83 | C． | 123 | D． | 564 |
12．执行如图所示的程序框图，如果输入的x、y∈R，那么输出的S的最大值为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
9．
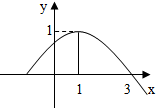函数y=sin（ωx+φ）（x∈R，ω＞0，0≤φ≤2π）的部分图象如图所示，则（ ）
函数y=sin（ωx+φ）（x∈R，ω＞0，0≤φ≤2π）的部分图象如图所示，则（ ）| A． | ω=$\frac{π}{2}$，φ=$\frac{π}{4}$ | B． | ω=$\frac{π}{3}$，φ=$\frac{π}{6}$ | C． | ω=$\frac{π}{4}$，φ=$\frac{π}{4}$ | D． | ω=$\frac{π}{4}$，φ=$\frac{5π}{4}$ |