题目内容
1.在直角坐标系中划出下列方程表示的图象(1)x2+2xy-3y2=0;(2)$\sqrt{{x}^{2}-4}$•$\sqrt{y+2}$=0;(3)|x|+|y|=1.
分析 (1)由因式分解可得(x+3y)(x-y)=0,可得图象为两条直线;
(2)方程等价为x2-4=0或y=-2,图象为三条直线;
(3)讨论x,y的符号,可得图象为四条线段构成的正方形.
解答 解:(1)x2+2xy-3y2=0,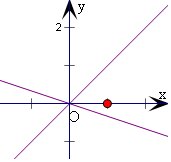
即为(x+3y)(x-y)=0,
即x=y或x=-3y,
图象如右图两条直线;
(2)$\sqrt{{x}^{2}-4}$•$\sqrt{y+2}$=0,
即为x2-4=0或y=-2,
即有x=±2,或y=-2,
图象如右下图三条直线;
(3)|x|+|y|=1,
当x≥0,y≥0时,可得x+y=1;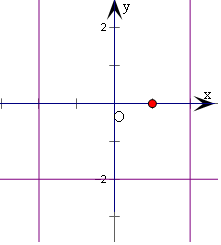
当x≤0,y≤0时,可得-x-y=1;
当x≥0,y≤0时,可得x-y=1;
当x≤0,y≥0时,可得-x+y=1.
图象如下图正方形ABCD.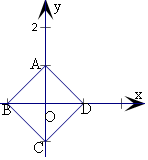
点评 本题考查方程表示的曲线,注意等价变形,考查数形结合思想方法,属于基础题.

练习册系列答案
相关题目
5.函数y=lg(2cosx-1)的定义域为( )
| A. | [-$\frac{π}{3}$,$\frac{π}{3}$] | B. | [2kπ-$\frac{π}{3}$,2kπ+$\frac{π}{3}$],k∈Z | ||
| C. | (-$\frac{π}{3}$,$\frac{π}{3}$) | D. | (2kπ-$\frac{π}{3}$,2kπ+$\frac{π}{3}$),k∈Z |
2.已知集合A={-2,-1,0,1,2},B={x|(x-1)(x+3)<0},则A∩B=( )
| A. | {-2,-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
10.“x<-2”是“($\frac{1}{2}$)${\;}^{{x}^{2}}$≥$\frac{1}{16}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.sin 110° cos40°-cos70°•sin40°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |