题目内容
已知函数f x=3sin2x+2
sinxcosx+5cos2x
(1)若f(α)=5,求tanα的值;
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,且(2a-c)cosB=bcosC,求函数f(x)在(0,B)上的最大值和最小值.
| 3 |
(1)若f(α)=5,求tanα的值;
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,且(2a-c)cosB=bcosC,求函数f(x)在(0,B)上的最大值和最小值.
考点:三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值,三角函数的图像与性质
分析:(1)化简可得解析式f(x)=2sin(2x+
)+4由f(α)=2sin(2α+
)+4=5,根据万能公式可解得tanα的值.
(2)已知等式(2a-c)cosB=bcosC,利用正弦定理可求得B=
.从而可得2x+
∈(
,
),即可求出函数f(x)在(0,B)上的最大值为6,最小值为5.
| π |
| 6 |
| π |
| 6 |
(2)已知等式(2a-c)cosB=bcosC,利用正弦定理可求得B=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(1)∵f(x)=3sin2x+2
sinxcosx+5cos2x
=
(1-cos2x)+
sin2x+
(1+cos2x)
=4+
sin2x+cos2x
=2sin(2x+
)+4
∴f(α)=2sin(2α+
)+4=5,可解得sin(2α+
)=
,即有
sin2α+cos2α=1
∴可得
+
=1,从而解得tanα=
或0.
(2)已知等式(2a-c)cosB=bcosC,利用正弦定理化简得:(2sinA-sinC)cosB=sinBcosC,
整理得:2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,
∴cosB=
,
则B=
.
∵x∈(0,
),∴2x+
∈(
,
)
∴sin(2x+
)∈(
,1)
∴2sin(2x+
)+4∈(5,6)
∴函数f(x)在(0,B)上的最大值为6,最小值为5.
| 3 |
=
| 3 |
| 2 |
| 3 |
| 5 |
| 2 |
=4+
| 3 |
=2sin(2x+
| π |
| 6 |
∴f(α)=2sin(2α+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
∴可得
2
| ||
| 1+tan2α |
| 1-tan2α |
| 1+tan2α |
| 3 |
(2)已知等式(2a-c)cosB=bcosC,利用正弦定理化简得:(2sinA-sinC)cosB=sinBcosC,
整理得:2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,
∴cosB=
| 1 |
| 2 |
则B=
| π |
| 3 |
∵x∈(0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴2sin(2x+
| π |
| 6 |
∴函数f(x)在(0,B)上的最大值为6,最小值为5.
点评:本题主要考查了三角函数中的恒等变换应用,正弦定理的应用,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
定义在R上的奇函数f(x)满足f(x+4)=f(x-2),则f(3)的值为( )
A、
| ||
| B、0 | ||
| C、3 | ||
| D、9 |
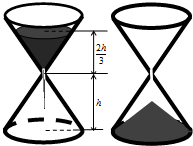 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的