题目内容
6.已知数列{an+n}是首项为2,公比为2的等比数列.(1)求数列{an}的通项公式;
(2)求a1+a2+a3+…+an的和.
分析 (1)利用等差数列通项公式先求出${a}_{n}+n={2}^{n}$,由此能求出数列{an}的通项公式.
(2)由${a}_{n}={2}^{n}-n$,利用分组求和法能求出a1+a2+a3+…+an.
解答 解:(1)∵数列{an+n}是首项为2,公比为2的等比数列,
∴${a}_{n}+n={2}^{n}$,
∴${a}_{n}={2}^{n}-n$.
(2)∵${a}_{n}={2}^{n}-n$,
∴a1+a2+a3+…+an
=(2+22+23+…+2n)-(1+2+3+…+n)
=$\frac{2(1-{2}^{n})}{1-2}$-$\frac{n(n+1)}{2}$
=2n+1-2-$\frac{n(n+1)}{2}$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
14.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值为( )
| A. | 5 | B. | 8 | C. | $\frac{13}{2}$ | D. | 7 |
11.对满足不等式组$\left\{\begin{array}{l}{x+1≥0}\\{x+y-4≤0}\\{x-y≤0}\end{array}\right.$的任意实数x,y,z=x2+y2-4x的最小值是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 6 |
18.若函数f(x)=ax2+bx+c满足f(1+x)=f(1-x),且f(0)<f(3),则( )
| A. | f(1)<c | B. | f(1)>c | C. | f(2)<c | D. | f(2)>c |
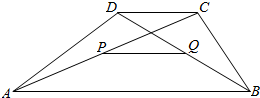 设P,Q分别是梯形ABCD的对角线AC与BD的中点
设P,Q分别是梯形ABCD的对角线AC与BD的中点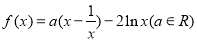 ,
,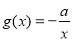 ,若至少存在一个
,若至少存在一个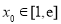 ,使
,使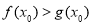 成立,则实数a的范围为( )
成立,则实数a的范围为( )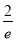 ,+∞) B.(0,+∞)
,+∞) B.(0,+∞)