题目内容
14.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值为( )| A. | 5 | B. | 8 | C. | $\frac{13}{2}$ | D. | 7 |
分析 根据两点的坐标写出斜率公式,求出m的值即可.
解答 解:经过两点(5,m)和(m,8)的直线的斜率等于1,
则$\frac{8-m}{m-5}$=1,
解得m=$\frac{13}{2}$,
∴m的值为$\frac{13}{2}$.
故选:C.
点评 本题考查了利用两点的坐标求斜率的应用问题,是基础题目.

练习册系列答案
相关题目
5.河中水流自西向东每小时10km,小船自南岸A点出发,想要沿直线驶向正北岸的B点,并使它的实际速度达到每小时10$\sqrt{3}$km,该小船行驶的方向和静水速度分别为( )
| A. | 西偏北30°,速度为20km/h | B. | 北偏西30°,速度为20km/h | ||
| C. | 西偏北30°,速度为20$\sqrt{3}$km/h | D. | 北偏西30°,速度为20$\sqrt{3}$km/h |
3.设α∈(π,2π),则$\sqrt{\frac{1-cos(π+α)}{2}}$等于( )
| A. | sin$\frac{α}{2}$ | B. | cos$\frac{α}{2}$ | C. | -sin$\frac{α}{2}$ | D. | -cos$\frac{α}{2}$ |
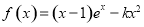 (其中
(其中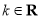 ).
).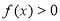 对
对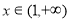 恒成立,求实数
恒成立,求实数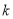 的取值范围;
的取值范围;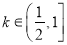 时,求函数
时,求函数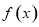 在
在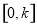 上的最大值
上的最大值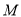 .
.