题目内容
11.对满足不等式组$\left\{\begin{array}{l}{x+1≥0}\\{x+y-4≤0}\\{x-y≤0}\end{array}\right.$的任意实数x,y,z=x2+y2-4x的最小值是( )| A. | -2 | B. | 0 | C. | 1 | D. | 6 |
分析 作出不等式组对应的平面区域,利用z的几何意义结合两点间的距离进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
z=x2+y2-4x=(x-2)2+y2-4
则z的几何意义为区域内的点到点D(2,0)的距离的平方-4,
由图象知D到直线x-y=0的距离为d=$\frac{|2-0|}{\sqrt{2}}=\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
此时z取得最小值为z=d2-4=2-4=-2,
故选:A.
点评 本题主要考查线性规划的应用,利用z的几何意义结合点到直线的距离公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.设α∈(π,2π),则$\sqrt{\frac{1-cos(π+α)}{2}}$等于( )
| A. | sin$\frac{α}{2}$ | B. | cos$\frac{α}{2}$ | C. | -sin$\frac{α}{2}$ | D. | -cos$\frac{α}{2}$ |
1.定义在R上的偶函数f(x),对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是( )
| A. | $(-\frac{1}{4},\frac{1}{4}]$ | B. | $(0,\frac{1}{4}]$ | C. | $(\frac{1}{4},\frac{1}{3}]$ | D. | $(0,\frac{1}{3})$ |
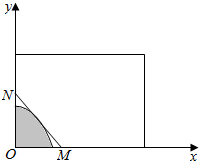 如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1.
如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1.