题目内容
定义max{a,b}=
(a,b∈R),若实数x,y满足
,则z=max{2x+3y-1,x+2y+2}的取值范围是( )
|
|
| A、[2,5] |
| B、[2,9] |
| C、[5,9] |
| D、[-1,9] |
考点:简单线性规划
专题:不等式的解法及应用
分析:先作出约束条件所对应的可行域,由Z=max{2x+3y-1,x+2y+2},当2x+3y-1≥x+2y+2即x+y-3≥0时的可行域即为图中△ABC可求Z的最大与最小值;当2x+3y-1<x+2y+2即x+y-3≥0时的可行域如图中的△OAC,Z=x+2y+2可求Z的最值,从而可求Z的范围.
解答:
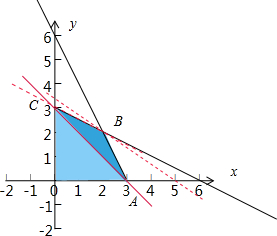 解:作出不等式组
解:作出不等式组
所表示的平面区域如图所示的OABC
当2x+3y-1≥x+2y+2即x+y-3≥0时的可行域即为图中△ABC,Z=2x+3y-1在B(2,2)处取得最大值9,在B(3,0)处取得最小值5,5≤Z≤9
当2x+3y-1<x+2y+2即x+y-3≥0时的可行域如图中的△OAC,Z=x+2y+2可在O(0,0)处取得最小值2,
在C(0,3)处取得最大值8
2≤Z≤8
综上可得,2≤Z≤9
故选:B.
 解:作出不等式组
解:作出不等式组
|
当2x+3y-1≥x+2y+2即x+y-3≥0时的可行域即为图中△ABC,Z=2x+3y-1在B(2,2)处取得最大值9,在B(3,0)处取得最小值5,5≤Z≤9
当2x+3y-1<x+2y+2即x+y-3≥0时的可行域如图中的△OAC,Z=x+2y+2可在O(0,0)处取得最小值2,
在C(0,3)处取得最大值8
2≤Z≤8
综上可得,2≤Z≤9
故选:B.
点评:本题主要考查了简单的线性规划,解题的关键是要根据题目中的定义确定目标函数及可行域的条件,属于知识的综合应用题.

练习册系列答案
相关题目
设x∈Z,集合A={x|x=2k-1,k∈Z},集合B={x|x=2k,k∈Z}.若命题p:?x∈A,2x∈B.则( )
| A、¬p:?x∈A,2x∉B |
| B、¬p:?x∉A,2x∉B |
| C、¬p:?x∉A,2x∈B |
| D、¬p:?x∈A,2x∉B |
已知P(0,1),O(0,0),A(1,0)为平面直角坐标系内的三点,若过点P的直线l与线段OA有公共点,则直线l的倾斜角的取值范围是( )
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
若关于x的方程(
)x=
有正数根,则实数a的取值范围是( )
| 1 |
| 2 |
| 1 |
| 1-lga |
| A、0<a<1 | B、a<1 |
| C、a≥1 | D、a>1 |
函数f(x)=log
(2x-3)的定义域为( )
| 1 |
| 2 |
| A、(2,+∞) | ||
| B、[2,+∞) | ||
C、(
| ||
D、[
|
下列对应是从A到B的函数的选项是( )
| A、A=B=N+,f:x→|x-3| |
| B、A={三角形},B={圆},f:三角形的内切圆 |
| C、A=R,B={1},f:x→y=1 |
| D、A=[-1,1],B=[-1,1],f:x→x2+y2=1 |
设i为虚数单位,则复数
的共轭复数为( )
| 2-4i |
| (1+i)2 |
| A、2+i | B、2-i |
| C、-2+i | D、-2-i |