题目内容
19.已知A={x|$\frac{1}{2}$<2x<4},B={x|log2(x-1)<2}.(1)求集合A和B
(2)求A∩B和A∪B.
分析 (1)利用指数函数的性质能求出集合A;
(2)利用交集和交集的性质求解
解答 解:(1)∵A={x|$\frac{1}{2}$<2x<4},B={x|log2(x-1)<2},
∴A={x|2-1<2x<22}={x|-1<x<2},
B={x|log2x(x-1)<log24}={x|$\left\{\begin{array}{l}{x-1>0}\\{x-1<4}\end{array}\right.$}={x|1<x<5}.
(2)A∩B={1<x<2},A∪B={-1<x5}.
点评 本题考查集合的求法,考查交集和并集的求法,是基础题,解题时要认真审题,注意不等式性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.有一个正三角形的两个顶点在抛物线y2=2px(p>0)上,另一顶点在原点,则该三角形的边长是( )
| A. | 2$\sqrt{3}$p | B. | 4$\sqrt{3}$p | C. | 6$\sqrt{3}$p | D. | 8$\sqrt{3}$p |
11.已知点P、A、B、C共面,点O不在该平面内,Sn是等差数列{an}的前n项和,且满足$\overrightarrow{OP}$=$\frac{1}{4}$a2•$\overrightarrow{OA}$+$\frac{1}{2}$a8•$\overrightarrow{OB}$+$\frac{1}{4}$a4008•$\overrightarrow{OC}$,则S2012的值为( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 2013 |
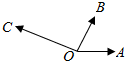 如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )
如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )