��Ŀ����
����ϸ�Ķ����²��ϣ�
��֪f��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�������������
��֤�����⡰��a��b��R+����ab��1����f(a)+f(b)��f(
)+f(
)���������⣮
֤�� ��Ϊa��b��R+����ab��1��a��
��0��
����Ϊf��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�������������
������f(a)��f(
)�� ��
ͬ����f(b)��f(
)�� ��
�ɢ�+�ڵ�f(a)+f(b)��f(
)+f(
)��
�ʣ����⡰��a��b��R+����ab��1����f(a)+f(b)��f(
)+f(
)���������⣮
����������Ķ������е�f��x��������������⣺
��1����������ĵȼ���֤��������a��b��R+����f(a)+f(b)��f(
)+f(
)����ab��1���������⣻
��2�������x�IJ���ʽf��ax-1��+f��2x����f��a1-x��+f��2-x��������a��0����
��֪f��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�������������
��֤�����⡰��a��b��R+����ab��1����f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
֤�� ��Ϊa��b��R+����ab��1��a��
| 1 |
| b |
����Ϊf��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�������������
������f(a)��f(
| 1 |
| b |
ͬ����f(b)��f(
| 1 |
| a |
�ɢ�+�ڵ�f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
�ʣ����⡰��a��b��R+����ab��1����f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
����������Ķ������е�f��x��������������⣺
��1����������ĵȼ���֤��������a��b��R+����f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
��2�������x�IJ���ʽf��ax-1��+f��2x����f��a1-x��+f��2-x��������a��0����
���㣺����������Ӧ��,��������,��������ʽ�Ľⷨ
ר�⣺���������ʼ�Ӧ��
��������1����д��ԭ�����������⣺��a��b��R+����ab��1����f(a)+f(b)��f(
)+f(
)������ԭ������ԭ�������������ǵȼ����⣬֤��ԭ������������Ϊ�����⣻
��2�����ã�1���Ľ����У�ax-1•2x��1��������2a��x��a���ٷ֢ٵ�2a��1ʱ���ڵ�0��2a��1ʱ���۵�2a=1ʱ���������д������ʽ�Ľ⼯��
| 1 |
| a |
| 1 |
| b |
��2�����ã�1���Ľ����У�ax-1•2x��1��������2a��x��a���ٷ֢ٵ�2a��1ʱ���ڵ�0��2a��1ʱ���۵�2a=1ʱ���������д������ʽ�Ľ⼯��
���
�⣺��1��ԭ������ԭ�������������ǵȼ����⣮
ԭ�����������⣺��a��b��R+����ab��1����f(a)+f(b)��f(
)+f(
)��
����֤��ԭ������������Ϊ�����⣺
��Ϊa��b��R+����ab��1���ã�0��a��
��
��f��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�����������
����f(a)��f(
)����1��
ͬ���У�f(b)��f(
)����2��
�ɣ�1��+��2���ã�f(a)+f(b)��f(
)+f(
)
����ԭ������������Ϊ������
����ԭ����Ϊ�����⣮
��2���ɣ�1���Ľ����У�ax-1•2x��1��������2a��x��a��
�ٵ�2a��1ʱ����a��
ʱ������ʽ�Ľ⼯Ϊ����log2aa��+�ޣ���
�ڵ�0��2a��1ʱ����0��a��
ʱ������ʽ�Ľ⼯Ϊ����-�ޣ�log2aa����
�۵�2a=1ʱ����a=
ʱ������ʽ�Ľ⼯Ϊ��R��
ԭ�����������⣺��a��b��R+����ab��1����f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
����֤��ԭ������������Ϊ�����⣺
��Ϊa��b��R+����ab��1���ã�0��a��
| 1 |
| b |
��f��x���Ƕ����ڣ�0��+�ޣ��ϵĵ�����������
����f(a)��f(
| 1 |
| b |
ͬ���У�f(b)��f(
| 1 |
| a |
�ɣ�1��+��2���ã�f(a)+f(b)��f(
| 1 |
| a |
| 1 |
| b |
����ԭ������������Ϊ������
����ԭ����Ϊ�����⣮
��2���ɣ�1���Ľ����У�ax-1•2x��1��������2a��x��a��
�ٵ�2a��1ʱ����a��
| 1 |
| 2 |
�ڵ�0��2a��1ʱ����0��a��
| 1 |
| 2 |
�۵�2a=1ʱ����a=
| 1 |
| 2 |
������������Ҫ������������ۺ�Ӧ�ã���ͬʱ����֤��������ķ��������У�ԭ������ԭ�������������ǵȼ������ǽ������Ĺؼ���

��ϰ��ϵ�д�
 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
�����Ŀ
��֪˫����C��
-
=1��a��0��b��0����һ�������߷�����y=-
x������һ��������������y2=-24x�����ϣ���˫���ߵķ���Ϊ��������
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
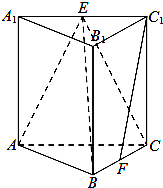 ��ͼ����������ABC-A1B1C1�У�CC1��ƽ��ABC��A1B1��BC��BC=1��
��ͼ����������ABC-A1B1C1�У�CC1��ƽ��ABC��A1B1��BC��BC=1��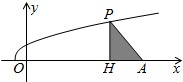 ��ͼ����֪��A��11��0��������y=
��ͼ����֪��A��11��0��������y=