题目内容
2．某几何体的三视图如图所示，则此几何体的外接球的表面积为（ ）
| A． | 8π | B． | 13π | C． | 17π | D． | 48π |
分析 如图所示，由三视图可知：该几何体为一个三棱锥．其中PA⊥底面ABC，BC⊥AC．该几何体的外接球的直径为PB．
解答 解：如图所示，由三视图可知：该几何体为一个三棱锥．
其中PA⊥底面ABC，BC⊥AC．
∴该几何体的外接球的直径为PB=$\sqrt{{2}^{2}+{3}^{2}+{2}^{2}}$=$\sqrt{17}$．
∴此几何体的外接球的表面积=4$π×（\frac{\sqrt{17}}{2}）^{2}$=17π．
故选：C．
点评 本题考查了三棱锥与球的三视图及其表面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．若全集U=R．A={x|1≤x≤5}．B={x|5≤x≤10}．则∁U（A∩B）=（ ）
| A． | {x|x≠5} | B． | {x|x=5} | C． | {x|x＜5} | D． | {x|x＞5} |
14．设函数f（x）=sin2（x+$\frac{π}{4}$）-cos2（x+$\frac{π}{4}$）（x∈R），则函数f（x）是（ ）
| A． | 最小正周期为π的奇函数 | B． | 最小正周期为π的偶函数 | ||
| C． | 最小正周期为$\frac{π}{2}$的奇函数 | D． | 最小正周期为$\frac{π}{2}$的偶函数 |
12．执行如图所示的程序框图，则输出m的值为（ ）
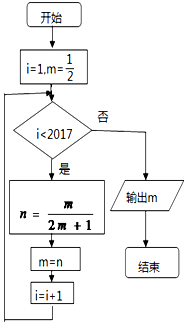
| A． | $\frac{1}{2016}$ | B． | $\frac{1}{2017}$ | C． | $\frac{1}{4032}$ | D． | $\frac{1}{4034}$ |