题目内容
13.已知等比数列{an}的各项均为正数,且a1>1,前n项之积为Tn,设T10=T20,(1)当n为何值时,Tn最大?
(2)是否存在自然数m,使得Tm=1?
分析 (1)设等比数列{an}的公比为q>0,且a1>1,由T10=T20,可得a11a12•…•a20=1,可得:${a}_{1}^{2}{q}^{19}$=1.于是Tn=${a}_{1}^{n}$•q1+2+…+(n-1)=${{a}_{1}}^{\frac{n(20-n)}{19}}$.利用二次函数的单调性即可得出.
(2)由Tn=${{a}_{1}}^{\frac{n(20-n)}{19}}$,可知:当n=20时,T20=1.
解答 解:(1)设等比数列{an}的公比为q>0,且a1>1,∵T10=T20,
∴a11a12•…•a20=1,
∴${a}_{1}^{10}$q10+11+…+19=${a}_{1}^{10}$q145=1,
∴${a}_{1}^{2}{q}^{19}$=1.
∴Tn=${a}_{1}^{n}$•q1+2+…+(n-1)=${a}_{1}^{n}{q}^{\frac{n(n-1)}{2}}$=${{a}_{1}}^{\frac{n(20-n)}{19}}$.
可知:当n=10时,指数$\frac{n(20-n)}{19}$取得最大值$\frac{100}{19}$,
∴当n=10时,Tn最大.
(2)由Tn=${{a}_{1}}^{\frac{n(20-n)}{19}}$,可知:当n=20时,T20=1.
点评 本题考查了等比数列的通项公式、指数的运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知$\overrightarrow{a}$=2,$\overrightarrow{b}$=1,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=5,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.函数y=3cosx是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
16.从[0,1]内随机取两个数a,b,则使a≥2b的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.
函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.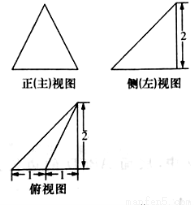
 B.
B.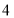 C.
C.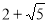 D.
D.