题目内容
(本小题满分13分)已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点 的距离之和为
的距离之和为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,
, ,且
,且 .若点
.若点 满足
满足 ,求
,求 的值.
的值.
(Ⅰ) ;(Ⅱ)-3或-1
;(Ⅱ)-3或-1
【解析】
试题分析:(Ⅰ)由已知 ,
, ,于是b=2,即得椭圆方程;(Ⅱ)点
,于是b=2,即得椭圆方程;(Ⅱ)点 为线段
为线段 的中垂线与直线
的中垂线与直线 的交点,先求出m=±2,然后分别写出AB的中垂线,令y=2即得x0的值.
的交点,先求出m=±2,然后分别写出AB的中垂线,令y=2即得x0的值.
试题解析:(Ⅰ)由已知 得
得 ,又
,又 .
.
∴ .
.
∴椭圆 的方程为
的方程为 . 4分
. 4分
(Ⅱ)由 得
得 ① 1分
① 1分
∵直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,∴△
,∴△ ,
,
得 .
.
设 ,
, ,则
,则 ,
, 是方程①的两根,
是方程①的两根,
则 ,
,  .
.
∴ .
.
又由 ,得
,得 ,解之
,解之 . 3分
. 3分
据题意知,点 为线段
为线段 的中垂线与直线
的中垂线与直线 的交点.
的交点.
设 的中点为
的中点为 ,则
,则 ,
, ,
,
?当 时,
时,
∴此时,线段 的中垂线方程为
的中垂线方程为 ,即
,即 .
.
令 ,得
,得 . 2分
. 2分
?当 时,
时,
∴此时,线段 的中垂线方程为
的中垂线方程为 ,即
,即 .
.
令 ,得
,得 . 2分
. 2分
综上所述, 的值为
的值为 或
或 .
.
考点:椭圆的标准方程,直线与椭圆的位置关系,平面向量

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 等于( )
等于( ) ,
, ,则
,则 = .
= .
 的图象大致为( )
的图象大致为( )
 :
: 在点
在点
 (
( )处的切线
)处的切线 的斜率为
的斜率为 ,直线
,直线 轴,
轴, 轴分别于点
轴分别于点 ,
, ,且
,且 .给出以下结论:
.给出以下结论: ;
; 时,
时, 的最小值为
的最小值为 ;
; 时,
时, ;
; 时,记数列
时,记数列 的前
的前 项和为
项和为 ,则
,则 .
.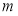 ,
,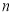 是两条不同直线,
是两条不同直线,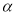 ,
,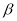 是两个不同的平面,且
是两个不同的平面,且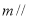
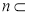
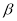 ,则下列叙述正确的是( )
,则下列叙述正确的是( )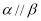 ,则
,则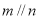
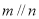 ,则
,则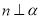 ,则
,则
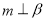 ,则
,则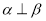
 是
是 所在平面上的两个定点,且满足
所在平面上的两个定点,且满足
 ,若
,若 ,则正实数
,则正实数 = .
= . ,若
,若 .
.