题目内容
已知曲线 :
: 在点
在点
 (
( )处的切线
)处的切线 的斜率为
的斜率为 ,直线
,直线 交
交 轴,
轴, 轴分别于点
轴分别于点 ,
, ,且
,且 .给出以下结论:
.给出以下结论:
① ;
;
②当 时,
时, 的最小值为
的最小值为 ;
;
③当 时,
时, ;
;
④当 时,记数列
时,记数列 的前
的前 项和为
项和为 ,则
,则 .
.
其中,正确的结论有 (写出所有正确结论的序号)
①③④
【解析】由题意,点P在抛物线C的上半部分,即曲线y= 上
上
y'= ,当x=0时,有l0=
,当x=0时,有l0= ,又l0与两坐标轴的截距绝对值相等,则l0=±1
,又l0与两坐标轴的截距绝对值相等,则l0=±1
所以 =1(负值舍去),于是a=1. ①正确;
=1(负值舍去),于是a=1. ①正确;
由a=1,有y= ,且y'=
,且y'= ,
,
于是在点Pn(n, )出的切线方程为y-
)出的切线方程为y- =
= (x-n)
(x-n)
令x=0,得yn=
因为n∈N*,故n=1时,yn取得最小值 ,②错误.
,②错误.
∵kn= (n∈N*),令t=
(n∈N*),令t= ∈(0,
∈(0, ]
]
设函数f(t)=t- sint,则f '(t)=1-
sint,则f '(t)=1- cost
cost
∵0<t≤ <
< ,故cost>
,故cost> ,于是f '(t)<0,即f(t)为减函数
,于是f '(t)<0,即f(t)为减函数
而f(0)=0,故t∈(0, ]时,f(t)<0,即t<
]时,f(t)<0,即t< sint
sint
也即kn= <
< sin
sin ,③正确.
,③正确.
由kn= ,设m=
,设m=
则m2=
故kn= <
<
故Sn=
<
= ,故④正确
,故④正确
考点:函数、导数、数列、不等式等综合应用

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
 的方程
的方程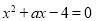 在区间
在区间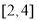 上有实数根,则实数
上有实数根,则实数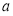 的取值范围是( )
的取值范围是( )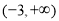 (B)
(B)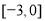 (C)
(C)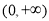 (D)
(D)
 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点 的距离之和为
的距离之和为 .
. 与椭圆
与椭圆 ,
, ,且
,且 .若点
.若点 满足
满足 ,求
,求 的值.
的值.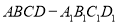 棱长为4,点
棱长为4,点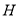 在棱
在棱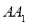 上,且
上,且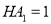 .在侧面
.在侧面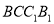 内作边长为1的正方形
内作边长为1的正方形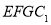 ,
,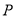 是侧面
是侧面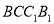 内一动点,且点
内一动点,且点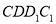 距离等于线段
距离等于线段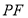 的长.则当点
的长.则当点 运动时,
运动时,  的最小值是 ( )
的最小值是 ( )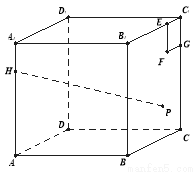
 (B)
(B) (C)
(C) (D)
(D)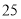
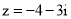 (
(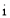 是虚数单位),则下列说法正确的是( )
是虚数单位),则下列说法正确的是( )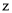 的虚部为
的虚部为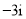
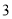
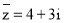
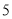
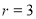 ,沿圆锥体的母线把侧面展开后得到一个圆心角为
,沿圆锥体的母线把侧面展开后得到一个圆心角为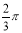 的扇形,则该圆锥体的表面积是 .
的扇形,则该圆锥体的表面积是 . 作圆
作圆 的两条切线,切点分别为A、B,则直线AB的方程为
的两条切线,切点分别为A、B,则直线AB的方程为 B.
B.
 D.
D.