题目内容
四边形 的内角
的内角 与
与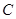 互补,
互补, .
.
(1)求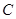 和
和 ;
;
(2)求四边形 的面积.
的面积.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)连接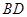 .在
.在 和
和 中,利用余弦定理列等式
中,利用余弦定理列等式
 和
和 ,且
,且 ,代入数据得
,代入数据得
 ,求
,求 的值,进而求
的值,进而求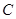 和
和 的值;(2)由(1)知
的值;(2)由(1)知 和
和 的面积可求,故四边形
的面积可求,故四边形 等于
等于 和
和 的面积.
的面积.
(1)由题设及余弦定理得
 .①
.①
 .②
.②
由①②得 ,故
,故 ,
, .
.
(2)四边形 的面积
的面积

 .
.
考点:1、余弦定理;2、诱导公式;3、三角形的面积公式.

练习册系列答案
相关题目
题目内容
四边形 的内角
的内角 与
与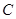 互补,
互补, .
.
(1)求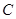 和
和 ;
;
(2)求四边形 的面积.
的面积.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)连接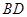 .在
.在 和
和 中,利用余弦定理列等式
中,利用余弦定理列等式
 和
和 ,且
,且 ,代入数据得
,代入数据得
 ,求
,求 的值,进而求
的值,进而求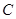 和
和 的值;(2)由(1)知
的值;(2)由(1)知 和
和 的面积可求,故四边形
的面积可求,故四边形 等于
等于 和
和 的面积.
的面积.
(1)由题设及余弦定理得
 .①
.①
 .②
.②
由①②得 ,故
,故 ,
, .
.
(2)四边形 的面积
的面积

 .
.
考点:1、余弦定理;2、诱导公式;3、三角形的面积公式.
